Goodhart’s Law is an adage which states the following:
“When a measure becomes a target, it ceases to be a good measure.”
This is particularly pertinent in machine learning, where the source of many of
our greatest achievements comes from optimizing a target in the form of a loss
function. The most prominent way to do so is with stochastic gradient descent
(SGD), which applies a simple rule, follow the gradient:
For some step size $alpha$. Updates of this form have led to a series of
breakthroughs from computer vision to reinforcement learning, and it is easy to
see why it is so popular: 1) it is relatively cheap to compute using backprop
2) it is guaranteed to locally reduce the loss at every step and finally 3) it
has an amazing track record empirically.
However, we wouldn’t be writing this if SGD was perfect! In fact there are some
negatives. Most importantly, there is an intrinsic bias towards ‘easy’
solutions (typically associated with high negative curvature). In some cases,
two solutions with the same loss may be qualitatively different, and if one is
easier to find then it is likely to be the only solution found by SGD. This has
recently been referred to as a “shortcut” solution [1], examples of which are
below:
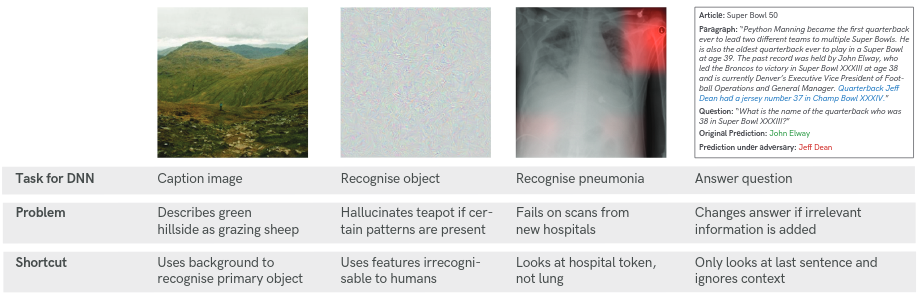
As we see, when classifying sheep, the network learns to use the green
background to identify the sheep present. When instead it is provided with an
image of sheep on a beach (which is an interesting prospect) then it fails
altogether. Thus, the key question motivating our work is the following:
Question: How can we find a diverse set of different solutions?
Our answer to this is to follow eigenvectors of the Hessian (‘ridges’) with
negative eigenvalues from a saddle, in what we call Ridge Rider (RR).
There is a lot to unpack in that statement, so we will go into more detail in
the following section.
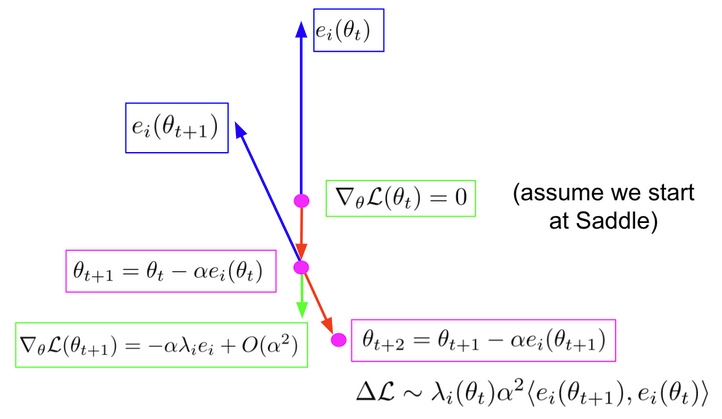
First, we assume we start at a saddle (green), where the norm of the gradient
is zero. We compute the eigenvectors and eigenvalues of the Hessian, which
solve the following:
And we follow the eigenvectors with negative eigenvalues, which we call ridges.
We can follow these in both directions. As you see in the diagram, when we take
a step along the ridge (in red) we reach a new point. Now the gradient is the
step size multiplied by the eigenvalue and the eigenvector, because the
eigenvector was of the Hessian. Now we re-compute the spectrum, and select the
new ridge as the one with the highest inner product with the previous, to
preserve the direction. We then take a step along a new ridge, to
$theta_{t+2}$.
So why do we do about this? Well, in the paper we show that if the inner
product between the new and the old ridge is greater than zero then we are
theoretically guaranteed to improve our loss. What this means is, RR provides
us with an orthogonal set of loss reducing directions. This is opposed to
SGD, which will almost always follow just one.
The full picture
In the next diagram we show the full Ridge Rider algorithm.

We begin at a Maximally Invariant Saddle (MIS) that retains and respects all of
the symmetries of the underlying problem. We branch, and select a ridge to
follow, which we update until we reach a breaking point where we branch again.
At this point we can choose whether to continue along the current path or
select another ridge from the buffer. This is equivalent to choosing between
breadth first search of depth first search. Finally the leaves of the tree are
the solutions to our problem, each is uniquely defined by the fingerprint.
On the positive side, RR provides us with a set of orthogonal locally
loss-reducing directions that can be used to span a tree of solutions. It
essentially turns optimization into a search problem, which allows us to
introduce new methods to use for finding solutions. We also benefit from the
natural ordering and grouping scheme provided by the eigenvalues (Fingerprint).
However, of course, there are many obvious questions that naturally arise with
this approach. Here we try to answer the FAQs:
Q: This seems expensive! Don’t you need loads of samples due to the high variance of Hessian?
A: Yes, that is fair! 🙁
Q: This seems expensive! Do you need to re-evaluate the full spectrum of the Hessian each timestep?
A: Actually no! We present an approximate version of RR using Hessian Vector
Products. We will go into this next.
We use the Power/Lanczos method in GetRidges. In UpdateRidge, after each step
along the ridge, we find the new $e_i, lambda_i$ pair by minimizing:
We warm-start with the 1st-order approximation to $lambda(theta)$, where
$theta’, lambda’, e_i’$ are the previous values:
These terms only rely on Hessian vector products!
Q: This seems expensive! Don’t you need to evaluate hundreds or thousands of branches?
A: We actually don’t. We show in the paper that symmetries lead to repeated
Eigenvalues, which reduces the number of branches we need to explore.
A symmetry, $phi$, of the loss function is a bijection on the parameter
space such that
We show that in the presence of symmetries, the Hessian has repeated
eigenvalues. This means we only have to explore one from each set!
RR in action: An illustrative example
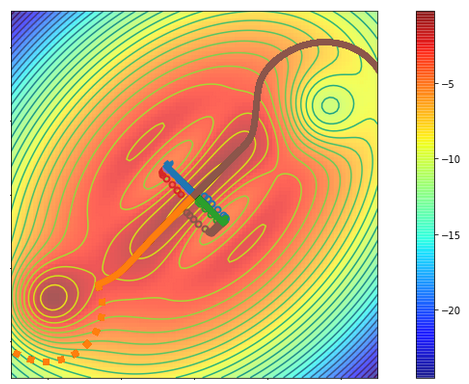
The Figure above shows a 2d cost surface, where we begin in the middle and want
to reach the blue areas. SGD always gets stuck in the valleys which correspond
to the locally steepest descent direction, this is shown by the circles. When
running RR, the first ridge also follows this direction, as we see in blue and
green. However, the second, orthogonal direction (brown and orange) avoids the
local optima and reaches the high value regions.
Ridge Rider for Exploration in Reinforcement Learning
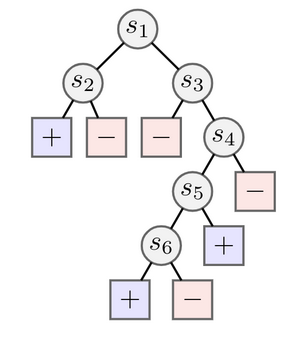
We tested RR in the tabular RL setting, where we sought to find diverse
solutions to a tree-based exploration task. We generated trees like the one
above, which has positive or negative rewards at the leaves. In this case we
see it is much easier to find the positive reward on the left, corresponding to
a policy which goes left at $s_1$ and left at $s_2$. To find the solution at
the bottom (going left from $s_6$) requires avoiding several negative rewards.
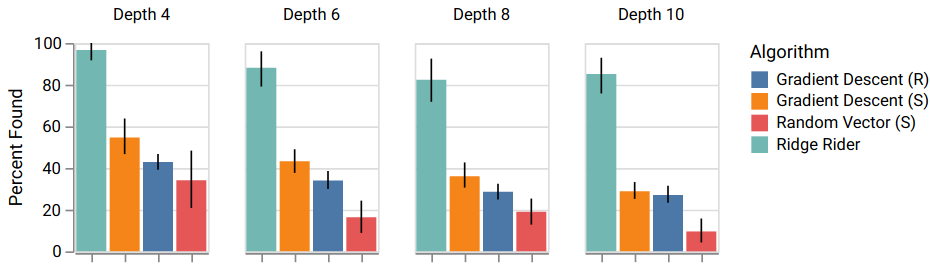
To rigorously evaluate RR, we generated 20 trees for four different depths, and
ran the algorithm each time, comparing against Gradient Descent starting from
random initializations or the MIS, and random vectors from the MIS. The results
show that RR on average finds almost all the solutions, while the other methods
fail to even find half.
In the paper we include additional ablations, and a first foray into
sample-based RL. We encourage you to check it out.
Ridge Rider for Supervised Learning
We wanted to test the approximate RR algorithm in the simplest possible
setting, which naturally brought us to MNIST, the canonical ML dataset! We used
the approximate version to train a neural network with two 128-unit hidden
layers, and surprisingly we were able to get 98% accuracy. This clearly isnt a
new SoTA for computer vision, but we think it is a nice result which shows the
possible scalability of our algorithm.
Interestingly, it seems the individual ridges correspond to learning different
features. In the next Figure, we show the performance for a classifier trained
by following each ridge individually.
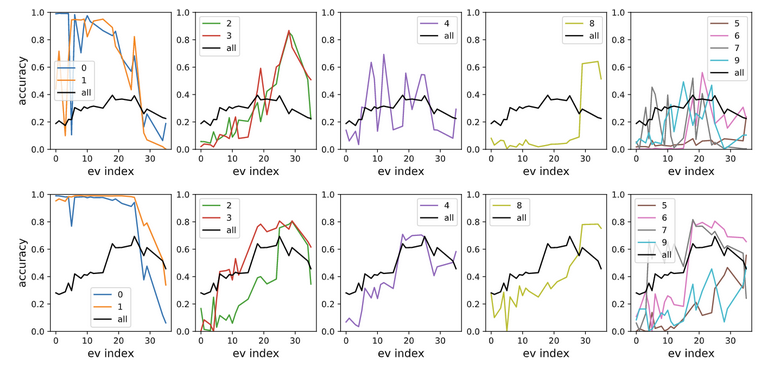
As we see, the earlier ridges correspond to learning 0 and 1, while the later
ones learn to classify the digit 8.
This provides further evidence that the Hessian contains structure which may
relate to causal information about the problem. Next we further develop this by
looking at out-of-distribution generalization.
Ridge Rider for Out of Distribution Generalization
We tested RR on the colored MNIST dataset, from [2]. Colored MNIST was
specifically designed to test causality, as each image is colored either red or
green in a way that correlates strongly (but spuriously) with the class label.
By construction, the label is more strongly correlated with the color than with
the digit. Any algorithm purely minimizing training error will tend to exploit
the color.
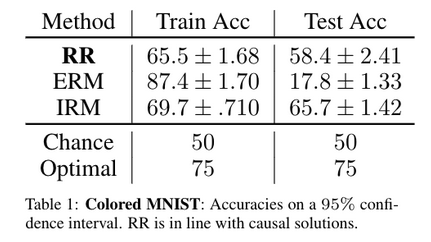
In the next Figure, we see that ERM (greedily optimizing the loss at training
time) massively overfits the problem, and does poorly at test time. By
contrast, RR achieves a respectable 58%, not too far from the 66% achieved by
the state-of-the-art causal approach.
Ridge Rider for Zero-Shot Co-ordination
Finally, we consider the zero-shot co-ordination problem. In this setting, we
wish to co-ordinate with a partner, but cannot see their policy in training.
Instead, we can agree on a training strategy, for example — which ridge to
follow.
We use an adapted version of the lever game from [3], shown below:
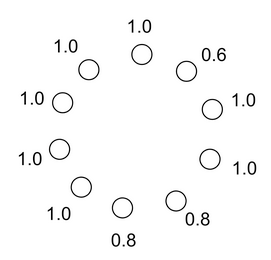
Recall from before that symmetries lead to repeated eigenvalues. This means the
levers which share a payoff with others will have the same eigenvalue.
Furthermore, the ordering of the ridges corresponding to repeated eigenvalues
is inconsistent across different runs. Thus, we can only coordinate reliably on
unique directions. We ran RR multiple times, and show the result for three
independent runs below.
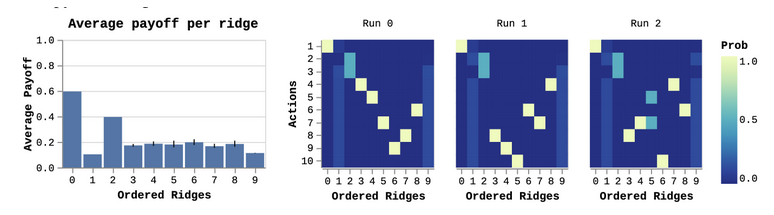
On the right, we see the first ridge is always the same action, which
corresponds to the optimal zero-shot solution. The next two are a 50-50 bet on
the two 0.8 ridges. The remaining ridges are largely a jumbled up mess,
corresponding to the levers with symmetries.
Summary and Future Work
A gif speaks a thousand words:

Paper:
- Ridge Rider: Finding Diverse Solutions by Following Eigenvectors of the Hessian.
Jack Parker-Holder, Luke Metz, Cinjon Resnick, Hengyuan Hu, Adam Lerer, Alistair Letcher, Alex Peysakhovich, Aldo Pacchiano, Jakob Foerster. NeurIPS 2020.
Paper Link
Code:
- RL: https://bit.ly/2XvEmZy
- ZS Co-ordination: https://bit.ly/308j2uQ
- OOD Generalization: https://bit.ly/3gWeFsH
References:
- [1] Robert Geirhos, Jörn-Henrik Jacobsen, Claudio Michaelis, Richard Zemel, Wieland Brendel, Matthias Bethge, Felix A. Wichmann (2020) Shortcut Learning in Deep Neural Networks.
- [2] Martin Arjovsky, Léon Bottou, Ishaan Gulrajani, David Lopez-Paz (2019) Invariant Risk Minimization. Arxiv pre-print.
- [3] Hengyuan Hu, Adam Lerer, Alex Peysakhovich, and Jakob Foerster. “Other-Play” for zero-shot coordination. International Conference on Machine Learning (ICML). 2020
