Many tasks that we do on a regular basis, such as navigating a city, cooking a
meal, or loading a dishwasher, require planning over extended periods of time.
Accomplishing these tasks may seem simple to us; however, reasoning over long
time horizons remains a major challenge for today’s Reinforcement Learning (RL)
algorithms. While unable to plan over long horizons, deep RL algorithms excel
at learning policies for short horizon tasks, such as robotic grasping,
directly from pixels. At the same time, classical planning methods such as
Dijkstra’s algorithm and A$^*$ search can plan over long time horizons, but
they require hand-specified or task-specific abstract representations of the
environment as input.
To achieve the best of both worlds, state-of-the-art visual navigation methods
have applied classical search methods to learned graphs. In particular, SPTM [2]
and SoRB [3] use a replay buffer of observations as nodes in a graph and learn
a parametric distance function to draw edges in the graph. These methods have
been successfully applied to long-horizon simulated navigation tasks that were
too challenging for previous methods to solve.
Nevertheless, these methods are still limited because they are highly sensitive
to errors in the learned graph. Even a single faulty edge acts like a wormhole
in the graph topology that planning algorithms try to exploit, which makes
existing methods that combine graph search and RL extremely brittle. For
example, if an artificial agent navigating a maze thinks that two observations
on either side of a wall are nearby, its plans will involve transitions that
collide into the wall. Adopting a simple model that assumes a constant
probability $p$ of each edge being faulty, we see that the expected number of
faulty edges is $p|E| = O(|V|^2)$. In other words, errors in the graph scale
quadratically with the number of nodes in the graph.
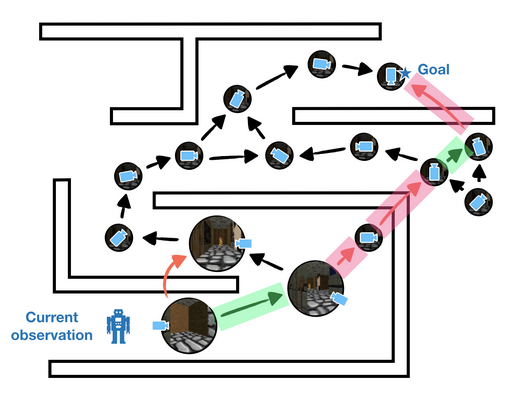
We could do a lot better if we could minimize the errors in the graph. But how?
Graphs over observations in both simulated and real-world environments can be
prohibitively large, making it challenging to even identify which edges are
faulty. To minimize errors in the graph, then, we desire sparsity; we want to
keep a minimal set of nodes that is sufficient for planning. If we have a way
to aggregate similar observations into a single node in the graph, we can
reduce the number of errors and improve the accuracy of our plans. The key
challenge is to aggregate observations in a way that respects temporal
constraints. If observations are similar in appearance but actually far away,
then they should be aggregated into different nodes.
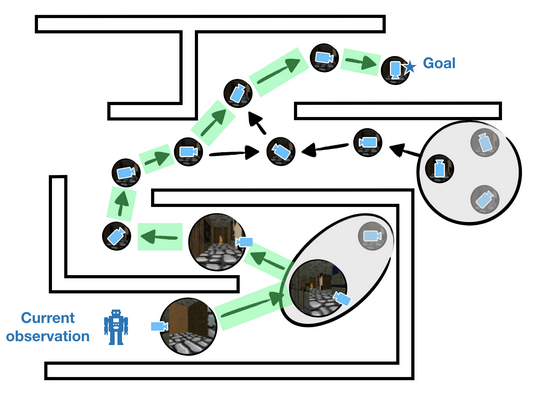
So how can we sparsify our graph while guaranteeing that the graph remains
useful for planning? Our key insight is a novel merging criterion called
two-way consistency. Two-way consistency can be viewed as a generalization of
value irrelevance to the goal-conditioned setting. Intuitively, two-way consistency
merges nodes (i) that can be interchanged as starting states and (ii) that can be
interchanged as goal states.
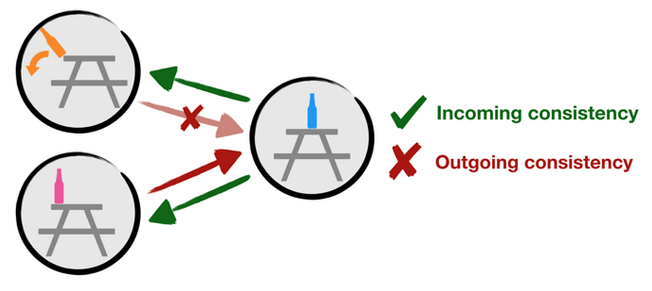
For an example of two-way consistency, consider the above figure. Suppose
during our node merging procedure we ask: can we merge the nodes with pink and
orange bottles according to two-way consistency? First, we note that moving
from the blue bottle to the pink bottle requires roughly the same work as
moving from the blue bottle to the orange bottle. So the nodes with pink and
orange bottles satisfy criterion (ii) because they can be interchanged as goal
states. However, while it is possible to start from the pink bottle and move to
the blue bottle, if we instead start at the orange bottle, the orange bottle
will fall to the floor and crash! So the nodes with pink and orange bottles
fail criterion (i) because they cannot be interchanged as starting states.
In practice, we can’t expect to encounter two nodes that can be perfectly
interchanged. Instead, we merge nodes that can be interchanged up to a
threshold parameter $tau$. By increasing $tau$, we can make the resulting
graph as sparse as we’d like. Crucially, *we prove in the paper that merging
according to two-way consistency preserves the graph’s quality up to an error
term that scales only linearly with the merging threshold $tau$.
Our motivation for sparsity, discussed above, is robustness: we expect smaller
graphs to have fewer errors. Furthermore, our main theorem tells us that we can
merge nodes according to two-way consistency while preserving the graph’s
quality. Experimentally, though, are the resulting sparse graphs more robust?
To test the robustness of Sparse Graphical Memory to errors in learned distance
metrics, we thinned the walls in the PointEnv mazes of [3]. While PointEnv is a
simple environment with $(x, y)$ coordinate observations, thinning the walls is
a major challenge for parametric distance functions; any error in the learned
distance function will cause faulty edges across the walls that destroy the
feasibility of plans. For this reason, simply thinning the maze walls is enough
to break the previous state-of-the-art [3] resulting in a 0% success rate.
How does Sparse Graphical Memory fare? With many fewer edges, it becomes
tractable to perform self-supervised cleanup: the agent can step through the
environment to detect and remove faulty edges from its graph. The below figure
illustrates the results of this process. While the dense graph shown in red has
many faulty edges, sparsity and self-supervised cleanup, shown in green,
overcome errors in the learned distance metric, leading to a 100% success rate.
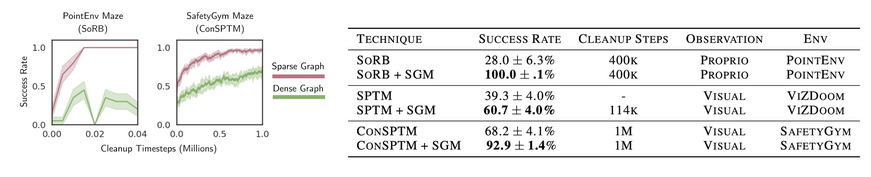
We see a similar trend in experiments with visual input. In both ViZDoom [4]
and SafetyGym [5] – maze navigation tasks that require planning from raw
images – Sparse Graphical Memory consistently improves the success of baseline
methods including SoRB [3] and SPTM [2].
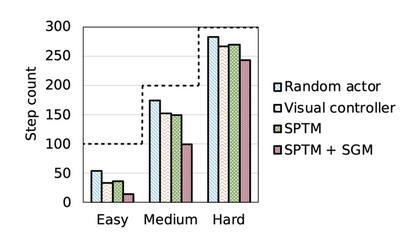
In addition to containing fewer errors, Sparse Graphical Memory also results in
more optimal plans. On a ViZDoom maze navigation task [4], we find that SGM
requires significantly less steps to reach the final goal across easy, medium,
and hard maze tasks, meaning that the agent follows a shorter path to the final
destination.
Overall, we found that state aggregation with two-way consistency resulted in
substantially more robust plans over the prior state-of-the-art. While
promising, many open questions and challenges remain for combining classical
planning with learning-based control. Some of the questions we’re thinking
about are – how can we extend these methods beyond navigation to manipulation
domains? As the world is not static, how should we build graphs over changing
environments? How can two-way consistency be utilized beyond the scope of
graphical-based planning methods? We are excited about these future directions
and hope our theoretical and experimental findings prove useful to other
researchers investigating control over extended time horizons.
References
- Emmons*, Jain*, Laskin* et al. Sparse Graphical Memory for Robust Planning. NeurIPS 2020.
- Savinov et al. Semi-parametric Topological Memory for Navigation. ICLR 2019.
- Eysenbach et al. Search on the Replay Buffer: Bridging Planning and Reinforcement Learning. NeurIPS 2020.
- Wydmuch et al. ViZDoom Competitions: Playing Doom from Pixels. IEEE Transactions on Games, 2018.
- Ray et al. Benchmarking Safe Exploration in Deep Reinforcement Learning. Preprint, 2019.
