Nearly all real-world applications of reinforcement learning involve some degree of shift between the training environment and the testing environment. However, prior work has observed that even small shifts in the environment cause most RL algorithms to perform markedly worse.
As we aim to scale reinforcement learning algorithms and apply them in the real world, it is increasingly important to learn policies that are robust to changes in the environment.
Broadly, prior approaches to handling distribution shift in RL aim to maximize performance in either the average case or the worst case. Methods such as domain randomization train a policy on a distribution of environments, and optimize the average performance of the policy on these environments. While this approach has been successfully applied to a number of areas
(e.g., self-driving cars, robot locomotion and manipulation),
its success rests critically on the design of the distribution of environments.
Moreover, policies that do well on average are not guaranteed to get high reward on every environment. The policy that gets the highest reward on average might get very low reward on a small fraction of environments. The second set of approaches, typically referred to as robust RL, focus on the worst-case scenarios. The aim is to find a policy that gets high reward on every environment within some set. Robust RL can equivalently be viewed as a two-player game between the policy and an environment adversary. The policy tries to get high reward, while the environment adversary tries to tweak the dynamics and reward function of the environment so that the policy gets lower reward. One important property of the robust approach is that, unlike domain randomization, it is invariant to the ratio of easy and hard tasks. Whereas robust RL always evaluates a policy on the most challenging tasks, domain randomization will predict that the policy is better if it is evaluated on a distribution of environments with more easy tasks.
Prior work has suggested a number of algorithms for solving robust RL problems. Generally, these algorithms all follow the same recipe: take an existing RL algorithm and add some additional machinery on top to make it robust.
For example, robust value iteration uses Q-learning as the base RL algorithm, and modifies the Bellman update by solving a convex optimization problem in the inner loop of each Bellman backup.
Similarly, Pinto ‘17 uses TRPO as the base RL algorithm and periodically updates the environment based on the behavior of the current policy. These prior approaches are often difficult to implement and, even once implemented correctly, they requiring tuning of many additional hyperparameters. Might there be a simpler approach, an approach that does not require additional hyperparameters and additional lines of code to debug?
To answer this question, we are going to focus on a type of RL algorithm known as maximum entropy RL, or MaxEnt RL for short (Todorov ‘06, Rawlik ‘08, Ziebart ‘10).
MaxEnt RL is a slight variant of standard RL aims to learn a policy that gets high reward while acting as randomly as possible; formally, MaxEnt maximizes the entropy of the policy. Some prior work has observed empirically that maximum entropy (MaxEnt) RL algorithms appear to be robust to some disturbances the environment.
To the best of our knowledge, no prior work has proven the folklore theorem that MaxEnt RL is robust to environmental disturbances.
In a recent paper, we prove that every MaxEnt RL problem corresponds to maximizing a lower bound on a robust RL problem. Thus, when you run MaxEnt RL, you are implicitly solving a robust RL problem. To the best of our knowledge, this is the first proof of that folklore theorem, and provides a theoretically-justified explanation for the empirical robustness of MaxEnt RL. In the rest of this post, we’ll provide some intuition into why MaxEnt RL should be robust and what sort of perturbations MaxEnt RL is robust to. We’ll also show some experiments demonstrating the robustness of MaxEnt RL.
<!–


(left) **Standard RL**: trained and evaluated without the obstacle.
(right) **MaxEnt RL**: trained and evaluated without the obstacle.
–>
| Standard RL | MaxEnt RL | |
|
Trained and evaluated without the obstacle: |

|

|
|
Trained without the obstacle, but evaluated with |

|

|
Intuition
So, why would we expect MaxEnt RL to be robust to disturbances in the environment? Recall that MaxEnt RL trains policies to not only maximize reward, but to do so while acting as randomly as possible. In essence, the policy itself is injecting as much noise as possible into the environment, so it gets to “practice” recovering from disturbances. Thus, if the change in dynamics appears like just a disturbance in the original environment, our policy has already been trained on such data. Another way of viewing MaxEnt RL is as learning many different ways of solving the task (Kappen ‘05). For example, let’s look at the task shown in videos above: we want the robot to push the white object to the green region. The top two videos show that standard RL always takes the shortest path to the goal, whereas MaxEnt RL takes many different paths to the goal. Now, let’s imagine that we add an obstacle (red blocks) to the environment that wasn’t included during training. As shown in the videos in the bottom row, the policy learned by standard RL almost always collides with the obstacle, rarely reaching the goal. In contrast, the MaxEnt RL policy often chooses routes around the obstacle, continuing to reach the goal for a large fraction of trials.
Theory
We now formally describe the technical results from the paper. The aim here is not to provide a full proof (see the paper Appendix for that), but instead to build some intuition for what the technical results say. Our main result is that, when you apply MaxEnt RL with some reward function and some dynamics, you are actually maximizing a lower bound on the robust RL objective. To explain this result, we must first define the MaxEnt RL objective:
$J_{MaxEnt}(pi; p, r)$ is the entropy-regularized cumulative return of policy $pi$ when evaluated using dynamics $p(s’ mid s, a)$ and reward function $r$. While we will train the policy using one dynamics $p$, we will evaluate the policy on a different dynamics, $tilde{p}$, chosen by the adversary. We can now formally state our main result as follows:
The left-hand-side is the robust RL objective. It says that the adversary gets
to whichever dynamics function $p$ makes our policy perform as poorly as
possible, subject to some constraints (as specified by the set $tilde{mathcal{P}}$). On
the right-hand-side we have the MaxEnt RL objective (note that $log T$ is a
constant, and the function $exp(cdots)$ is always increasing). Thus, this objective
says that a policy that has a high entropy-regularized reward (right hand-side)
is guaranteed to also get high reward when evaluated on an adversarially-chosen
dynamics.
The most important part of this equation is the set $tilde{mathcal{P}}$ of dynamics that
the adversary can choose from; our analysis describes precisely how this set is
constructed and shows that, if we want a policy to be robust to a larger set of
disturbances, all we have to do is increase the weight on the entropy term and
decrease the weight on the reward term. Intuitively, the adversary must choose
dynamics that are “close” to the dynamics on which the policy was trained. For
example, in the special case where the dynamics are linear-Gaussian, this set
corresponds to all perturbations where the original expected next state and the
perturbed expected next state have a Euclidean distance less than $epsilon$.
<!–
stuff
more stuff
The policy learned by MaxEntRL is robust to perturbations of the puck (red frames).
–>
|
Standard RL |
MaxEnt RL |

|

|
The policy learned by MaxEntRL is robust to perturbations of the puck (red frames).
More Experiments
Our analysis predicts that MaxEnt RL should be robust to many types of
disturbances. The first set of videos showed that MaxEnt RL is robust to new,
static obstacles. MaxEnt RL is also robust to perturbations introduced in the
middle of an episode. To demonstrate this, we took the same robotic pushing task
and knocked the puck out of place in the middle of the episode. The videos above
show that the policy learned by MaxEnt RL is more robust at handling these
perturbations, as predicted by our analysis.

|

|
|
|
Standard RL |
MaxEnt RL |
Evaluation on adversarial perturbations |
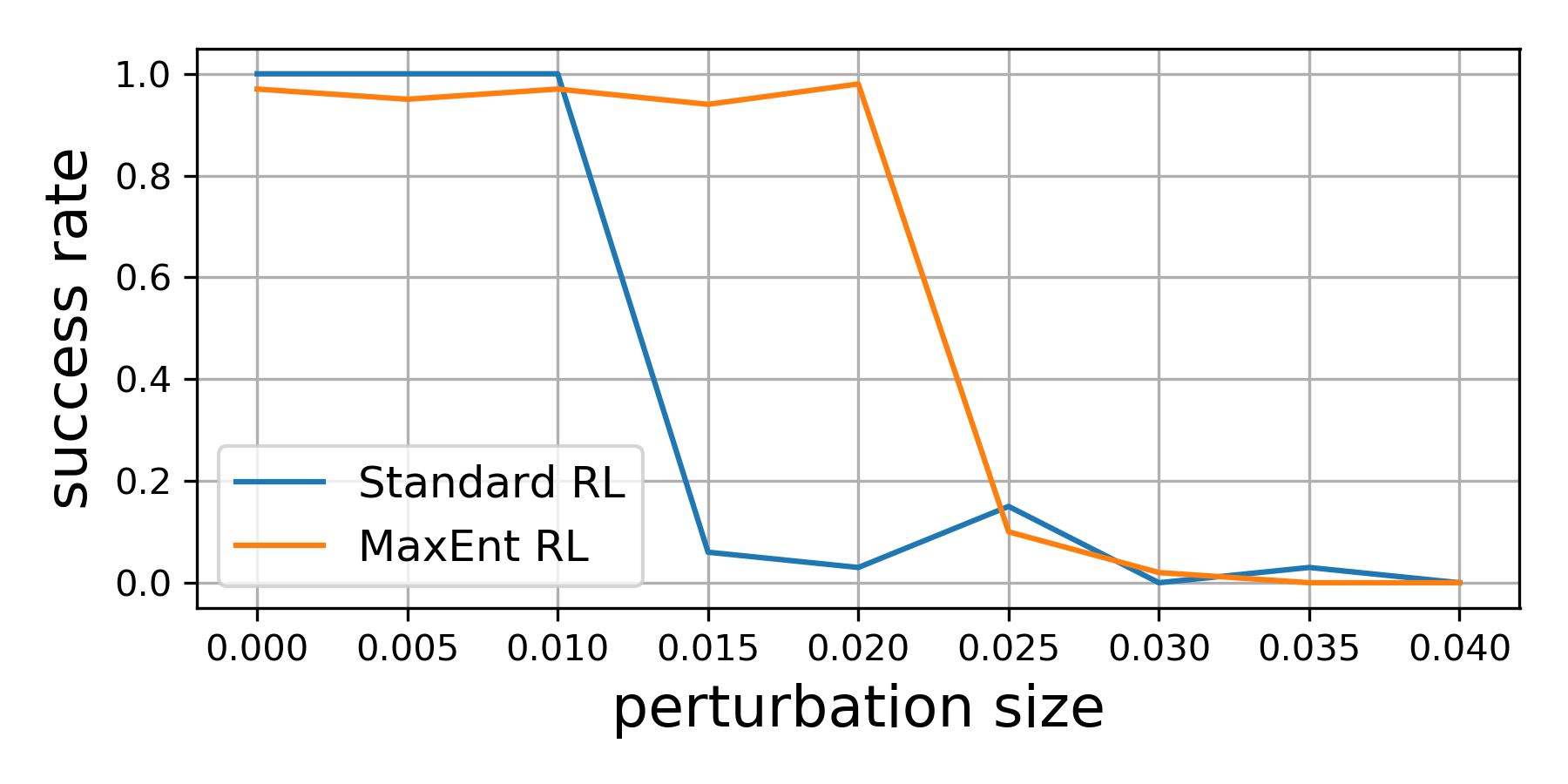
Our theoretical results suggest that, even if we optimize the environment
perturbations so the agent does as poorly as possible, MaxEnt RL policies will
still be robust. To demonstrate this capability, we trained both standard RL and
MaxEnt RL on a peg insertion task shown above. During evaluation, we changed the
position of the hole to try to make each policy fail. If we only moved the hole
position a little bit ($le$ 1 cm), both policies always solved the task. However,
if we moved the hole position up to 2cm, the policy learned by standard RL
almost never succeeded in inserting the peg, while the MaxEnt RL policy
continued to succeed for more than 95% of trials. This experiment validates our
theoretical findings that MaxEnt really is robust to (bounded) adversarial
disturbances in the environment.
Conclusion
In summary, this paper shows that a commonly-used type of RL algorithm, MaxEnt
RL, is already solving a robust RL problem. We do not claim that MaxEnt RL will
outperform purpose-designed robust RL algorithms. However, the striking
simplicity of MaxEnt RL compared with other robust RL algorithms suggests that
it may be an appealing alternative to practitioners hoping to equip their RL
policies with an ounce of robustness.
Acknowledgements
Thanks to Gokul Swamy, Diba Ghosh, and Colin Li for feedback on draft of post,
and to Chloe Hsu and Daniel Seita for help with the blog.
