This post is cross-listed on the CMU ML blog.

The history of machine learning has largely been a story of increasing
abstraction. In the dawn of ML, researchers spent considerable effort
engineering features. As deep learning gained popularity, researchers then
shifted towards tuning the update rules and learning rates for their
optimizers. Recent research in meta-learning has climbed one level of
abstraction higher: many researchers now spend their days manually constructing
task distributions, from which they can automatically learn good optimizers.
What might be the next rung on this ladder? In this post we introduce theory
and algorithms for unsupervised meta-learning, where machine learning
algorithms themselves propose their own task distributions. Unsupervised
meta-learning further reduces the amount of human supervision required to solve
tasks, potentially inserting a new rung on this ladder of abstraction.

We start by discussing how machine learning algorithms use human supervision to
find patterns and extract knowledge from observed data. The most common machine
learning setting is regression, where a human provides labels $Y$ for a set of
examples $X$. The aim is to return a predictor that correctly assigns
labels to novel examples. Another common machine learning problem setting is
reinforcement learning (RL), where an agent takes actions in an environment.
In RL, humans indicate the desired behavior through a reward function that
the agent seeks to maximize. To draw a crude analogy to regression,
the environment dynamics are the examples $X$, and the reward function gives
the labels $Y$. Algorithms for regression and RL employ many tools,
including tabular methods (e.g., value iteration), linear methods (e.g., linear
regression) kernel-methods (e.g., RBF-SVMs), and deep neural networks. Broadly, we call these
algorithms learning procedures: processes that take as input a dataset
(examples with labels, or transitions with rewards) and output a function that
performs well (achieves high accuracy or large reward) on the dataset.

Machine learning research is similar to the control room for large physics
experiments. Researchers have a number of knobs they can tune which affect the
performance of the learning procedure. The right setting for the knobs depends
on the particular experiment: some settings work well for high-energy
experiments; others work well for ultracold atom experiments.
Figure Credit.

Similar to lab procedures used in physics and biology, the learning
procedures used in machine learning have many knobs¹ that can be tuned.
For example, the learning procedure for training a neural network might be defined by an optimizer
(e.g., Nesterov, Adam) and a learning rate (e.g., 1e-5).
Compared with regression, learning procedures specific to RL (e.g., DDPG) often have many more knobs, including
the frequency of data collection and how frequently the policy is updated.
Finding the right setting for the knobs can have a large effect on how quickly
the learning procedure solves a task, and a good configuration of knobs for one
learning procedure may be a bad configuration for another.

Meta-Learning Optimizes Knobs of the Learning Procedure

While machine learning practitioners often carefully tune these knobs by hand,
if we are going to solve many tasks, it may be useful to automatic this
process. The process of setting the knobs of learning procedures via
optimization is called meta-learning [Thrun 1998]. Algorithms that perform this optimization
problem automatically are known as meta-learning algorithms.
Explicitly tuning the knobs of learning procedures is an active area of research, with various researchers looking at tuning the update rules [Andrychowicz 2016, Duan 2016, Wang 2016], weight initialization [Finn 2017], network weights [Ha 2016], network architectures [Gaier 2019], and other facets of learning procedures.

To evaluate a setting of knobs, meta-learning algorithms consider not one task
but a distribution over many tasks. For example, a distribution over supervised
learning tasks may include learning a dog detector, learning a cat detector,
and learning a bird detector. In reinforcement learning, a task distribution
could be defined as driving a car in a smooth, safe, and efficient manner,
where tasks differ by the weights they place on smoothness, safety, and
efficiency. Ideally, the task distribution is designed to mirror the
distribution over tasks that we are likely to encounter in the real world.
Since the tasks in a task distribution are typically related, information from
one task may be useful in solving other tasks more efficiently. As you might
expect, a knob setting that works best on one distribution of tasks may not be
the best for another task distribution; the optimal knob setting
depends on the task distribution.

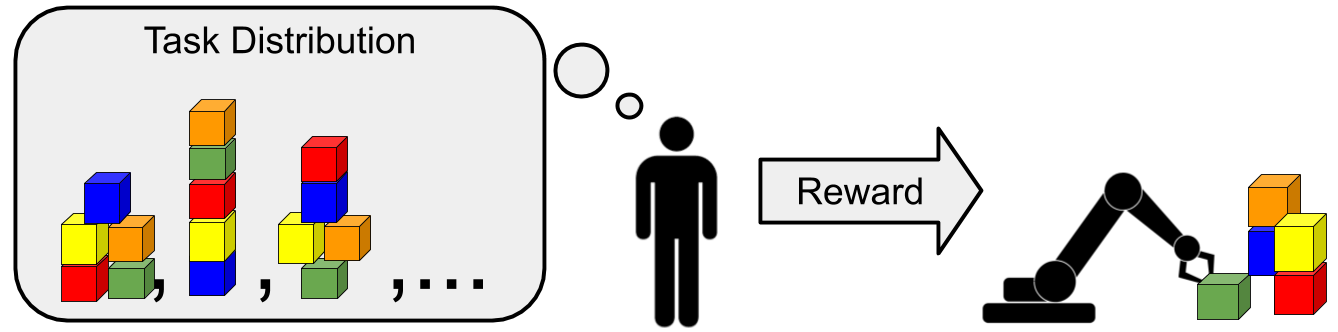
An illustration of meta-learning, where tasks correspond to arranging blocks
into different types of towers. The human has a particular block tower in mind
and rewards the robot when it builds the correct tower. The robot’s aim is to
build the correct tower as quickly as possible.

In many settings we want to do well on a task distribution to which we have
only limited access. For example, in a self-driving car, tasks may correspond
to finding the optimal balance of smoothness, safety, and efficiency for each
rider, but querying riders to get rewards is expensive. A researcher can
attempt to manually construct a task distribution that mimics the true task
distribution, but this can be quite challenging and time consuming. Can we
avoid having to manually design such task distributions?

To answer this question, we must understand where the benefits of meta-learning
come from. When we define
task distributions for meta-learning, we do so with some prior knowledge in
mind. Without this prior information, tuning the knobs of a learning procedure
is often a zero-sum game: setting the knobs to any configuration will
accelerate learning on some tasks while slowing learning on other tasks. Does
this suggest there is no way to see the benefit of meta-learning without the
manual construction of task distributions? Perhaps not! The next section
presents an alternative.

Optimizing the Learning Procedure with Self-Proposed Tasks

If designing task distributions is the bottleneck in applying meta-learning
algorithms, why not have meta-learning algorithms propose their own tasks? At
first glance this seems like a terrible idea, because the No Free Lunch Theorem
suggests that this is impossible, without additional knowledge. However, many
real-world settings do provide a bit of additional information, albeit
disguised as unlabeled data. For example, in regression, we might have
access to an unlabeled dataset and know that the downstream tasks will be
labeled versions of this same image dataset. In a RL setting, a robot can
interact with its environment without receiving any reward, knowing that
downstream tasks will be constructed by defining reward functions for this very
environment (i.e. the real world). Seen from this perspective, the recipe for
unsupervised meta-learning (doing meta-learning without manually constructed
tasks) becomes clear: given unlabeled data, construct task distributions from this unlabeled data or environment, and then meta-learn to quickly solve these self-proposed tasks.

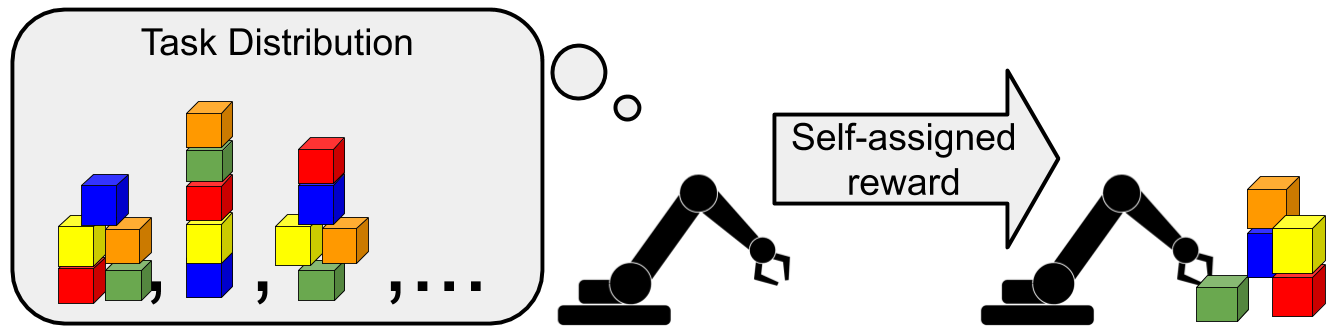
In unsupervised meta-learning, the agent proposes its own tasks, rather than
relying on tasks proposed by a human.

How can we use this unlabeled data to construct task distributions which will
facilitate learning downstream tasks? In the case of regression, prior work on
unsupervised meta-learning [Hsu 2018, Khodadadeh 2019] clusters an unlabeled dataset of images and then randomly chooses subsets of
the clusters to define a distribution of classification tasks. Other work
[Jabri 2019] look at an RL setting: after exploring an environment without a
reward function to collect a set of behaviors that are feasible in this
environment, these behaviors are clustered and used to define a distribution of
reward functions. In both cases, even though the tasks constructed can be
random, the resulting task distribution is not random, because all tasks share
the underlying unlabeled data — the image dataset for regression and
the environment dynamics for reinforcement learning. The underlying unlabeled
data are the inductive bias with which we pay for our free lunch.

Let us take a deeper look into the RL case. Without knowing the downstream tasks or reward functions, what is the “best” task distribution for “practicing” to solve tasks quickly? Can we measure how effective a task distribution is for solving unknown,
downstream tasks? Is there any sense in which one unsupervised task
proposal mechanism is better than another? Understanding the answers to these
questions may guide the principled development of meta-learning algorithms with
little dependence on human supervision. Our work [Gupta 2018], takes a
first step towards answering these questions. In particular, we examine the
worst-case performance of learning procedures, and derive an optimal
unsupervised meta-reinforcement learning procedure.

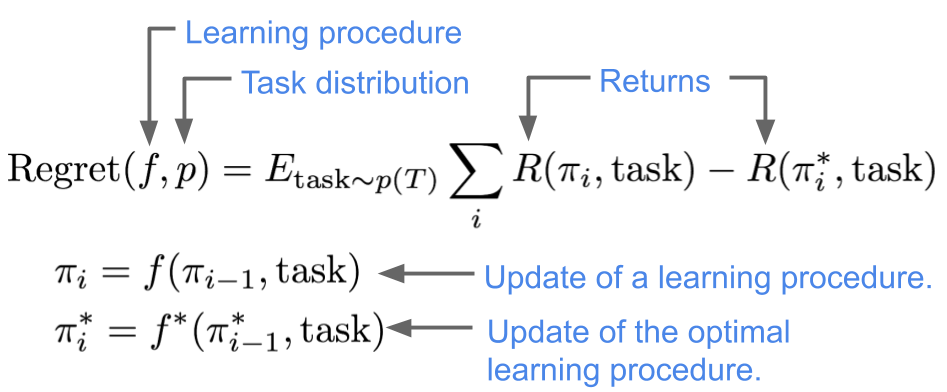
Optimal Unsupervised Meta-Learning

To answer the questions posed above, our first step is to define an optimal
meta-learner for the case where the distribution of tasks is known.
We define an optimal meta-learner as the learning procedure that achieves the
largest expected reward, averaged across the distribution of tasks. More precisely,
we will compare the expected reward for a learning procedure $f$
to that of best learning procedure $f^*$,
defining the regret of $f$ on a task distribution $p$ as follows:

Extending this definition to the case of unsupervised meta-learning, an optimal
unsupervised meta-learner can be defined as a meta-learner that achieves the
minimum worst-case regret across all possible task distributions that may be
encountered in the environment. In the absence of any knowledge about the
actual downstream task, we resort to a worst case formulation. An unsupervised
meta-learning algorithm will find a single learning procedure $f$ that has the
lowest regret against an adversarially chosen task distribution $p$:

Our work analyzes how exactly we might obtain such an optimal unsupervised
meta-learner, and provides bounds on the regret that it might incur in the
worst case. Specifically, under some restrictions on the family of tasks that
might be encountered at test-time, the optimal distribution for an unsupervised
meta-learner to propose is uniform over all possible tasks.

The intuition for this is straightforward: if the test time task distribution
can be chosen adversarially, the algorithm must make sure it is uniformly good
over all possible tasks that might be encountered. As a didactic example, if
test-time reward functions were restricted to the class of goal-reaching tasks,
the regret for reaching a goal at test-time is inverse related to the probability
of sampling that goal during training-time. If any one of
the goals $g$ has lower density than the others, an adversary can propose
a task distribution solely consisting of reaching that goal $g$
causing the learning procedure to incur a higher regret. This example suggests that we can find an optimal unsupervised meta-learner using a uniform distribution over goals. Our paper formalizes this idea and extends it to broader classes task distributions.

Now, actually sampling from a uniform distribution over all possible tasks is quite challenging.
Several recent papers have proposed RL exploration methods based on maximizing
mutual information [Achiam 2018, Eysenbach 2018, Gregor 2016, Lee 2019, Sharma 2019].
In this work, we show that these methods provide a tractable approximation to the uniform distribution over task distributions. To
understand why this is, we can look at the form of a mutual information
considered by [Eysenbach 2018], between states $s$ and latent
variables $z$:

In this objective, the first marginal entropy term is maximized when there is a
uniform distribution over all possible tasks. The second conditional entropy
term ensures consistency, by making sure that for each $z$, the resulting
distribution of $s$ is narrow. This suggests constructing unsupervised
task-distributions in an environment by optimizing mutual information
gives us a provably optimal task distribution, according to our
notion of min-max optimality.

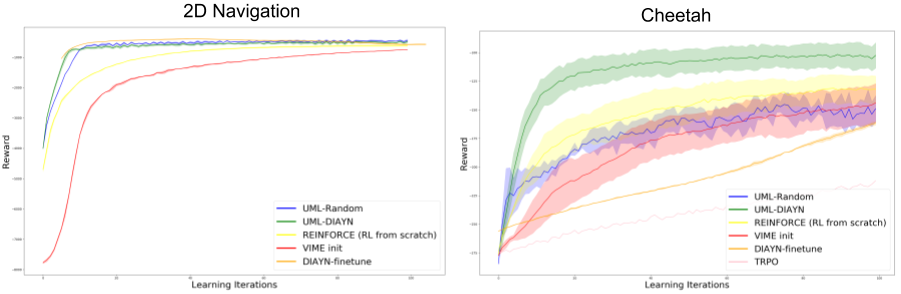
While the analysis makes some limiting assumptions about the forms of tasks
encountered, we show how this analysis can be extended to provide a bound on
the performance in the most general case of reinforcement learning. It also
provides empirical gains on several simulated environments as compared to
methods which train from scratch, as shown in the Figure below.

Summary & Discussion

In summary:

• Learning procedures are recipes for converting datasets into function
  approximators. Learning procedures have many knobs, which can be tuned by
  optimizing the learning procedures to solve a distribution of tasks.

• Manually designing these task distributions is challenging, so a recent line
  of work suggests that the learning procedure can use unlabeled data to
  propose its own tasks for optimizing its knobs.

• These unsupervised meta-learning algorithms allow for learning in regimes
  previously impractical, and further expand that capability of machine
  learning methods.

• This work closely relates to other works on unsupervised skill
  discovery, exploration and representation learning, but
  explicitly optimizes for transferability of the representations and skills to
  downstream tasks.

A number of open questions remain about unsupervised meta-learning:

• Unsupervised learning is closely connected to unsupervised meta-learning: the
  former uses unlabeled data to learn features, while the second uses unlabeled
  data to tune the learning procedure. Might there be some unifying treatment
  of both approaches?

• Our analysis only proves that task proposal based on mutual information is optimal for memoryless meta-learning algorithms. Meta-learning algorithms with memory, which we expect will perform better, may perform best with different task proposal mechanisms.

• Scaling unsupervised meta learning to leverage large-scale datasets and
  complex tasks holds the promise of acquiring learning procedures for solving
  real-world problems more efficiently than our current learning procedures.

Check out our paper for more experiments and proofs: https://arxiv.org/abs/1806.04640

Acknowledgments

Thanks to Jake Tyo, Conor Igoe, Sergey Levine, Chelsea Finn, Misha Khodak, Daniel Seita, and Stefani Karp for their feedback.

Read More