In this post, we present an optimized Triton BF16 Grouped GEMM kernel for running training and inference on Mixture-of-Experts (MoE) models, such as DeepSeekv3.
A Grouped GEMM applies independent GEMMs to several slices (groups) of an input tensor in a single kernel call. In a baseline Pytorch implementation, these GEMMS would be carried out in a for-loop over the groups, with one kernel launch per iteration.
Our kernel achieves up to 2.62x speedup over the manual PyTorch loop implementation on NVIDIA H100 GPUs when used in DeepSeekv3 training. We discuss the Triton kernel optimization techniques we leveraged and showcase end-to-end results.
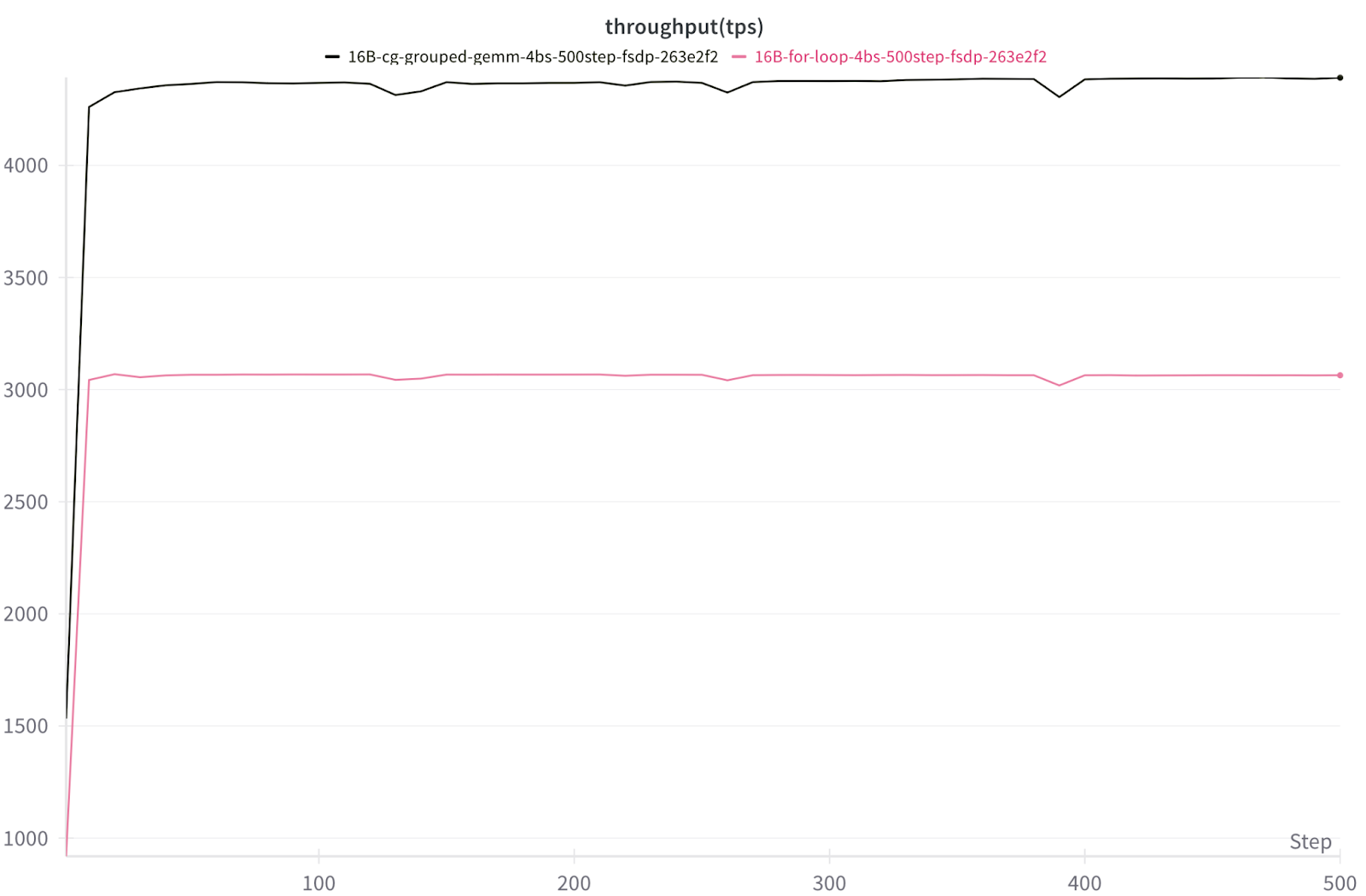
16B DeepSeekv3 TPS throughput on 8x NVIDIA H100 with FSDP2
Triton Kernel Grouped Gemm vs PyTorch manual looping Group GEMM (1.42x-2.62x Speedup)
Background
GEMM (General Matrix Multiplication) is a fundamental primitive in LLM workloads. When an input activation matrix is multiplied by a weight matrix, a GEMM is being performed. In modern deep learning based architectures, GEMMs dominate FLOP counts, so their efficiency often defines end-to-end model speed.
In Mixture-of-Expert (MoE) models, tokens are dynamically routed to different experts which results in many independent GEMMs. A Grouped GEMM executes multiple smaller GEMMs together in one kernel launch. Instead of treating each expert or layer as a separate GEMM, we batch them, which reduces launch overhead and improves GPU utilization.

Figure 1. Example GEMM problem with 3 experts
To illustrate this, we can imagine a toy scenario where we have 3 expert weights and a varying number of tokens being routed to each expert, so the activations are of different sizes. We can construct these 3 matrix multiplications of varying sizes into a single Grouped GEMM problem, which allows us to calculate the output matrices C1, C2, and C3 in a single kernel launch.
Optimization 1: Persistent Kernel Design
Nvidia GPUs have streaming multiprocessor units (SMs) that contain specialized hardware units to perform load, store, and compute operations. SM utilization is key to kernel performance. Thus, when implementing parallel algorithms such as Grouped Matrix-Multiplication using the Triton programming language, a key consideration is the work decomposition across SMs.
In a naive work division, a new threadblock (CTA) would be launched for every tile of work. In contrast, persistent kernels keep CTAs “alive” and dynamically feed them new tiles until the entire GEMM is complete. This avoids launch overhead, improves cache reuse, and reduces scheduling imbalance, which can lead to an effect known as wave quantization. Wave quantization is an inefficiency that occurs when the number of output tiles are not evenly divisible by the number of GPU SMs which leads to low utilization. This Colfax post provides a deep dive into the topic.
We build on this idea by applying the persistent kernel strategy in our Group GEMM kernel. In training and prefill workloads for MoE models, the matrix multiplication problem sizes are large. Thus, in naive work decomposition, a large number of threadblocks need to be scheduled to compute the output matrix, which would result in multiple “waves” of work being done. Instead, with our persistent kernel design, we can compute the entire matrix multiplication in a single wave of work by making two key changes in our Triton kernel, as discussed in the code snippets below.
First, we set the kernel grid to be equal to the number of SMs on the H100 GPU, 132.
grid = (NUM_SMS, 1, 1) (Host Code)
Next, we change the outer for loop structure to:
for tile_id in tl.range(start_pid, num_tiles, NUM_SMS) (Device Code)
We launch one Triton program per SM, so all the Triton programs fit in a single wave with none waiting in the queue. Inside the kernel, each program loops over its share of tiles, fetching new work until all tiles are computed. This design keeps Triton programs alive on the SMs, eliminating repeated launches and making the GEMM a single continuous wave of work.
Optimization 2: Grouped Launch Ordering
An important consideration for kernel speed is cache performance. In Triton, the programmer controls the order in which the output tiles are computed, and thus, we can optimize L2 Cache performance at the kernel level. We experimented with both linear tile ordering (row major) and grouped launch ordering schedules. To illustrate the difference between these two approaches, we can examine the following toy matrix multiplication example, where A and B are the input matrices and C is the output matrix.
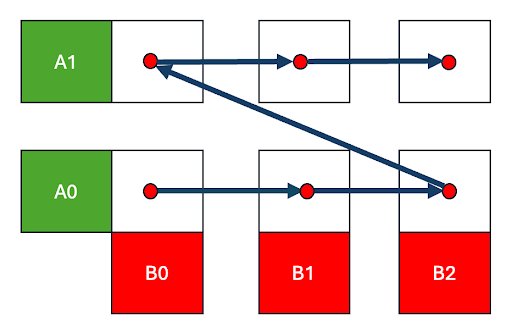
Figure 2. Row-Major Schedule
In the row-major traversal across the output C matrix, we move quickly across the columns of the B matrix and C(0,0) -> C(0,1) -> C(0,2) before moving to the next row, C(1,0). This means that B tiles will only be re-visited after cycling through an entire row of C, by which time the data may have been evicted.
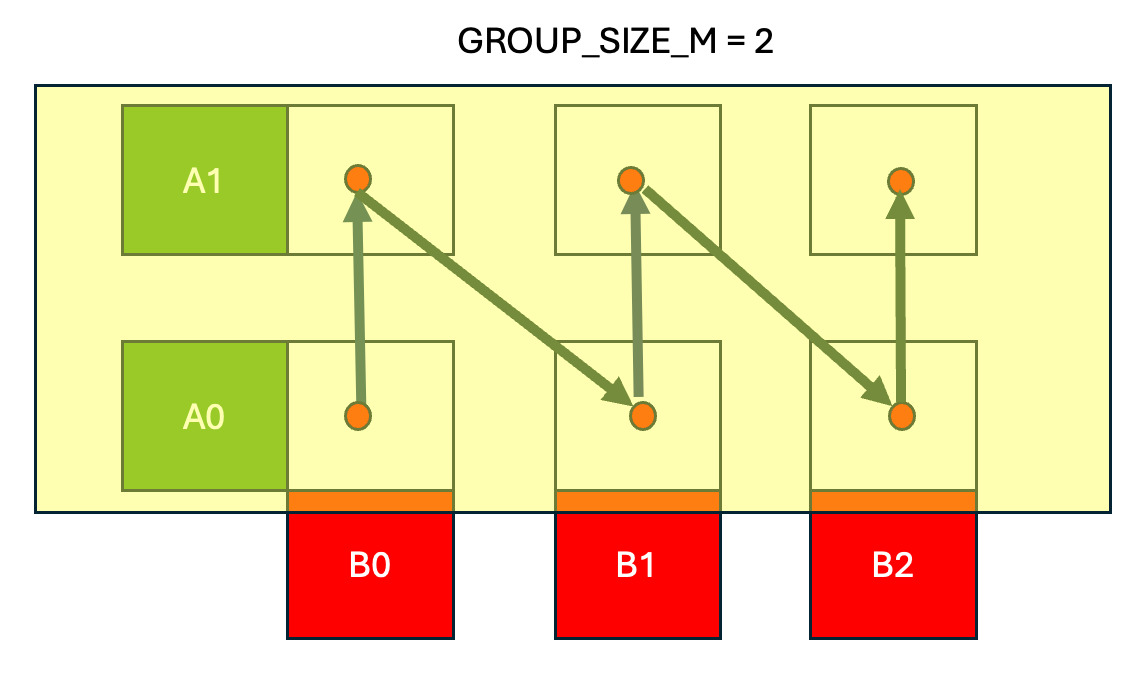
Figure 3. Grouped Launch Schedule with Group Size = 2
In the grouped launch schedule we hold a band of rows (=2) in Figure 3, from the A matrix in cache and traverse column-major across the output C matrix computing C(0,0) -> C(1,0) ->…-> C(GROUP_SIZE_M, 0) before moving to the next column and computing C(0,1) -> C(1,1) etc.
The net effect is that the grouped launch schedule increases cache performance for both A and B matrices. Consecutive Triton programs (CTAs) reuse the same B tile in quick succession while keeping a band of A rows in cache.
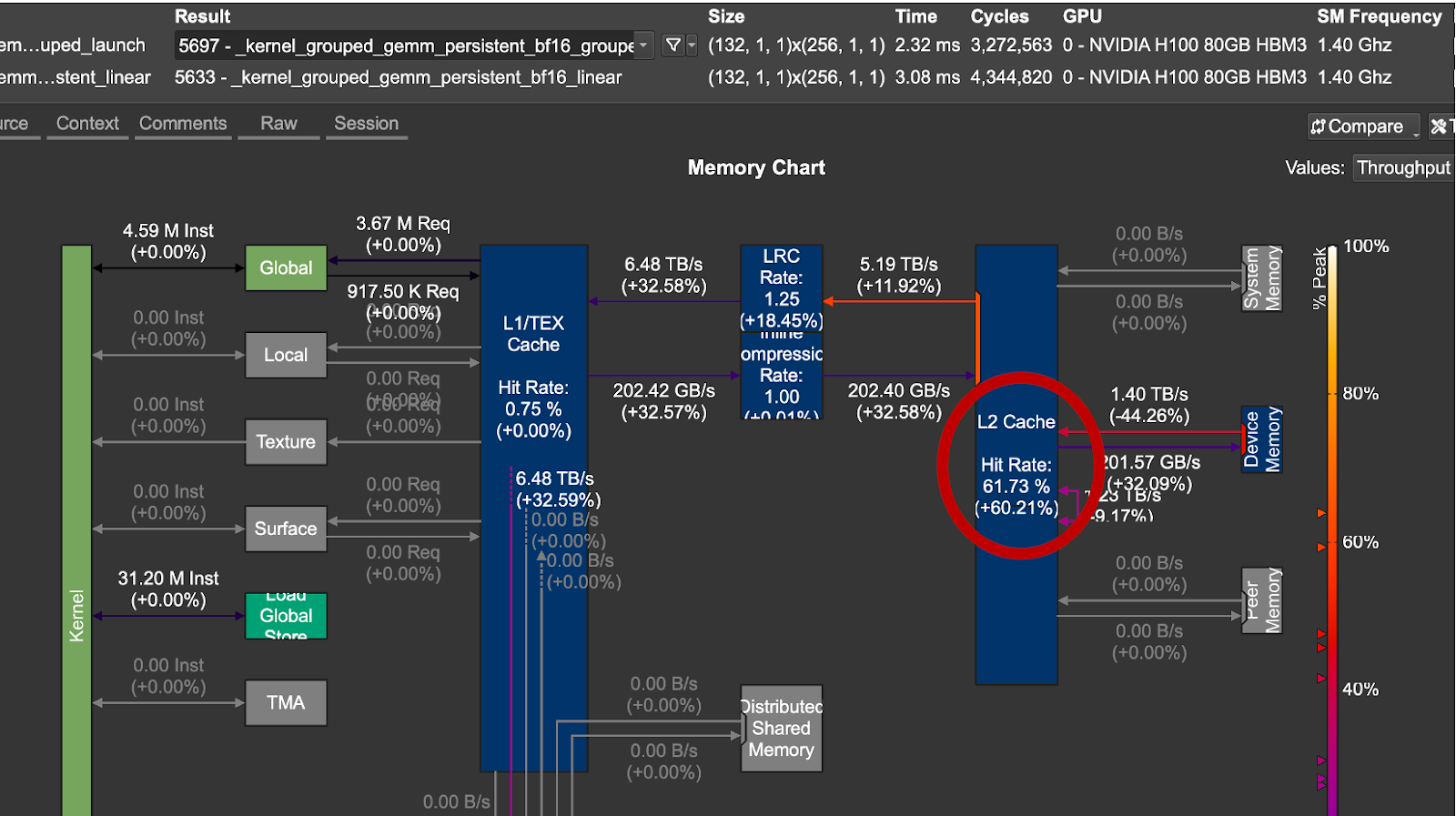
Figure 4. L2 Cache Gain for Grouped Launch Order vs Linear Launch Order
num_groups, m, k, n = 8, 4096, 2048, 7168
For the problem sizes we tested, the group launch ordering proved more performant in terms of date reuse and latency. From the above figure 4, we note a 1.33x speedup and a +60% in L2 Cache Hit Rate with the optimized schedule.
The main benefit of using the grouped launch schedule in our Group GEMM kernel is that it enforces temporal locality as exemplified in the illustrations above. This is achieved by re-ordering the launch order of programs so that tiles of the GEMM problem are computed in an order that allows for better reuse of the input activation and the expert weights, improving L2 cache hit rates, increasing arithmetic intensity, and thus reducing kernel latency.
Optimization 3: Tensor Memory Accelerator (TMA) utilization for Expert Weights
The TMA unit on NVIDIA Hopper GPUs is a dedicated hardware unit for load/store operations that operate on tensors. The benefit of leveraging the TMA unit in our kernel design is it can free up SM resources such as registers and CUDA cores while data is being moved from global to shared memory. To learn more about TMA usage in Triton, see our previous deep dive on this topic.
However, there is a caveat due to the special use case of this kernel. Typically, a TMA descriptor containing tensor metadata is created on the host and then passed to the kernel.
For MoE models, a modified approach is needed since the chosen expert is not known ahead of time. Instead, it is determined at runtime, creating a data-dependent access into the expert weight matrix. This type of access is possible in Triton by dynamically creating a local TMA descriptor based on the chosen expert index. We walk through the code below on how to build a TMA 2D descriptor on the device for the chosen expert, and then how to use it to issue TMA loads.
First, we pre-allocate a chunk of GPU memory, workspace, on the host:
workspace = torch.empty( NUM_SMS * desc_helper.tma_size, (Host Code) device=x.device, dtype=torch.uint8, )
The size of the memory we are reserving is equal to the size in bytes of a single TMA descriptor, desc_helper.tma_size, multiplied by the number of persistent Triton programs we are launching, NUM_SMs. This ensures that each Triton program will have space to write its own TMA descriptor.
expert_desc_ptr_tile = workspace + start_pid * TMA_SIZE tl.extra.cuda.experimental_device_tensormap_create2d( desc_ptr= expert_desc_ptr_tile, global_address=b_ptr + expert_idx*N*K + n_start*K, (Device Code) load_size=[BLOCK_SIZE_N, BLOCK_SIZE_K], global_size=[NUM_EXPERTS*N, K], element_ty=tl.bfloat16) tl.extra.cuda.experimental_tensormap_fenceproxy_acquire(expert_desc_ptr_tile) expert_weight = tl._experimental_descriptor_load( expert_desc_ptr_tile, [0, k_offset], [BLOCK_SIZE_N, BLOCK_SIZE_K], tl.bfloat16)
In the Triton code, each triton program first creates a private slot in workspace to place the expert descriptor. Next, we create a 2D tensor map that points to the routed expert tile by passing the experts metadata. Then, we explicitly call a proxy fence, which is required to synchronize memory operation between two different proxies, SM and TMA engine. In our kernel, every time a new expert_idx is selected the SM writes a new TMA descriptor to global memory. The fence guarantees that the new TMA descriptor is globally visible before the TMA engine issues a load instruction. This ensures we are not reading stale/incorrect data.
Now, since the TMA descriptors have been constructed dynamically based on the chosen expert_idx each Triton program in the Grouped GEMM kernel can target its TMA load to the routed expert weight.
Microbenchmarks
We benchmarked our Hopper-optimized kernel against a baseline Triton Group GEMM kernel that does not contain the optimizations we discussed to isolate the gain from these techniques.
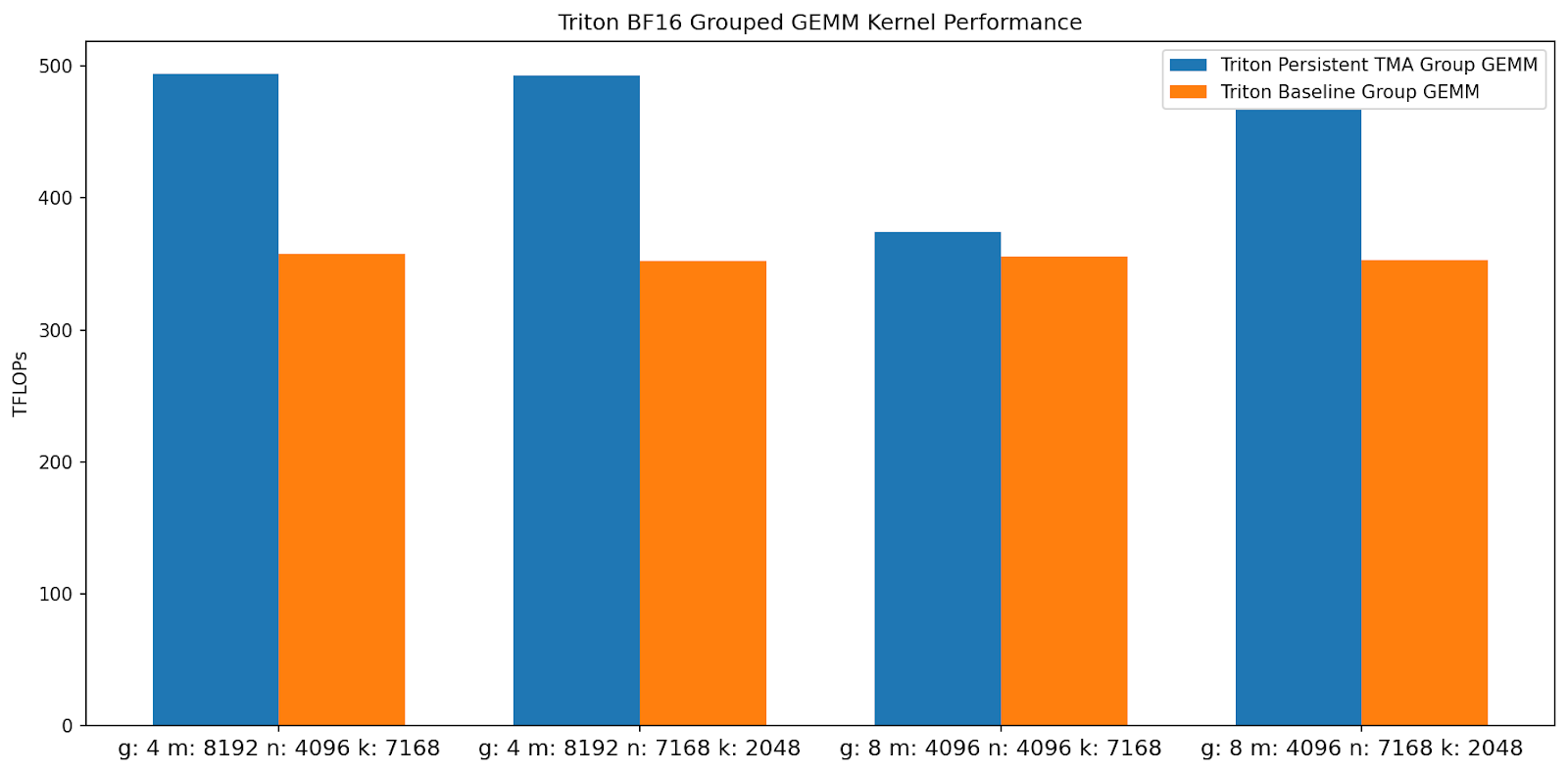
Figure 5. Triton Group GEMM Kernel TFLOPs Comparison (Higher is Better)
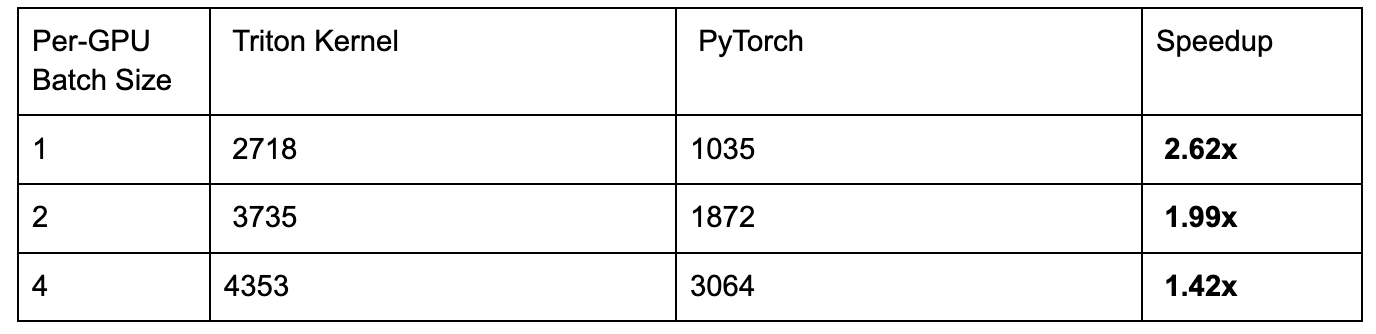
Figure 6. Kernel Latency Comparison with Speedup over Baseline Triton Kernel
By leveraging a persistent kernel design, grouped launch tile ordering, and the Hopper TMA unit, our kernel achieves up to 1.50x speedup over the baseline Triton kernel.
End-to-End Benchmarks
We integrated our kernel into torchtitan to create an end-to-end test in which we train a 16B parameter flavor of DeepSeekv3 using FSDP2 across 8xH100’s. The speedups for various batch sizes are below:

Figure 7. 16B DeepSeekv3 E2E Tokens/s/GPU Throughput Summary
MoE models have a much higher parameter-to-flops ratio than dense models, and this fact makes FSDP2 suboptimal for training due to the cost of communicating large weights. It is instead more beneficial to parallelize by statically placing different experts on different GPUs and communicating activations around. The number of tokens processed by each GPU changes dynamically in such Expert Parallel training, which makes the use of triton kernels challenging, since every new token count may require kernel recompilation, depending on the details of the implementation. We leave support for such dynamic training workloads to future work.
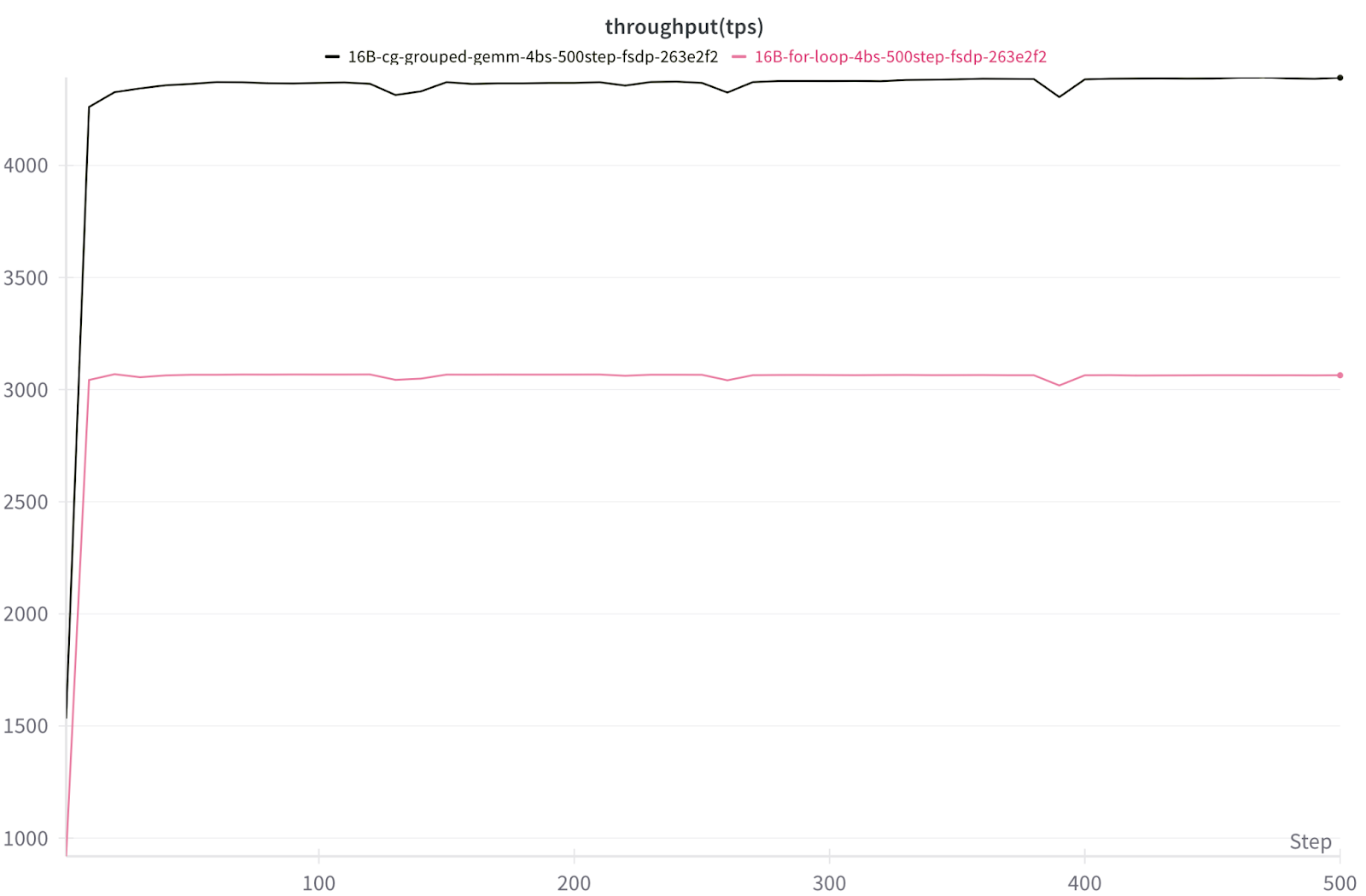
Training (torchtitan)
Figure 8. Tokens/s/GPU for batch-size 4, 16B DeepSeekv3 on 8x NVIDIA H100 with FSDP2
Training (torchtitan)
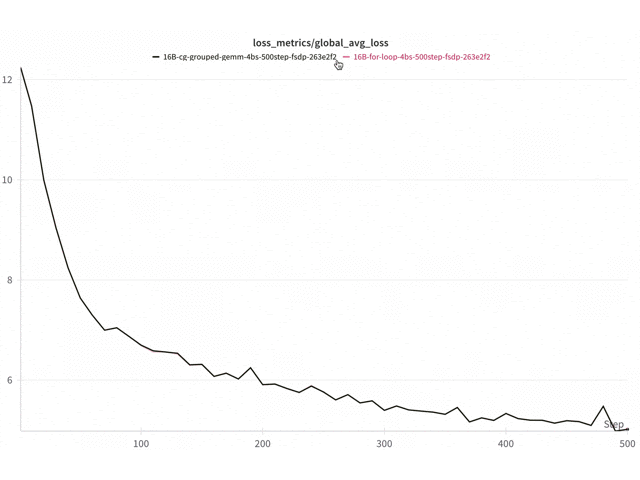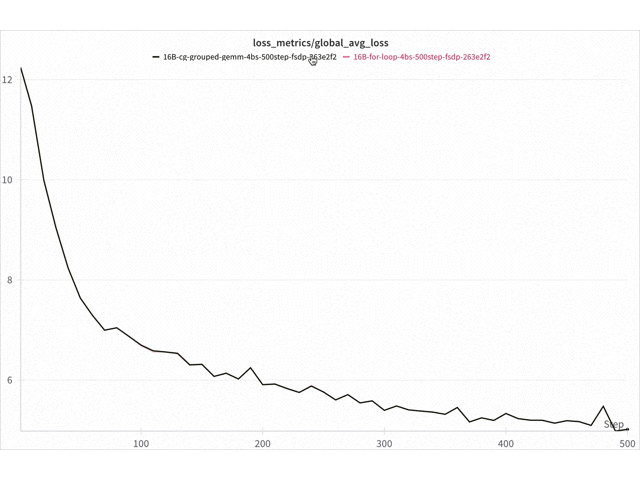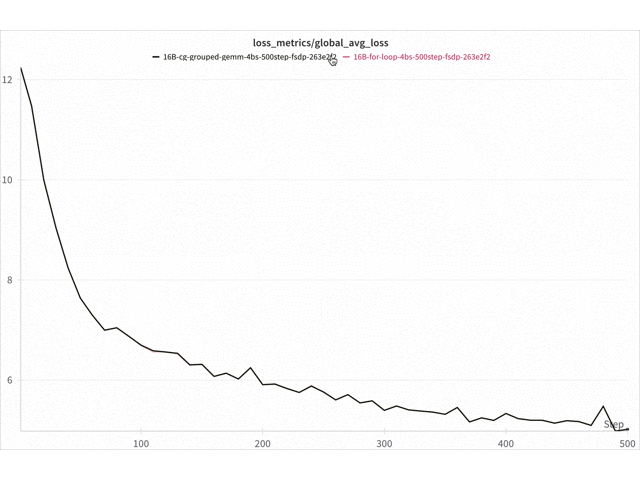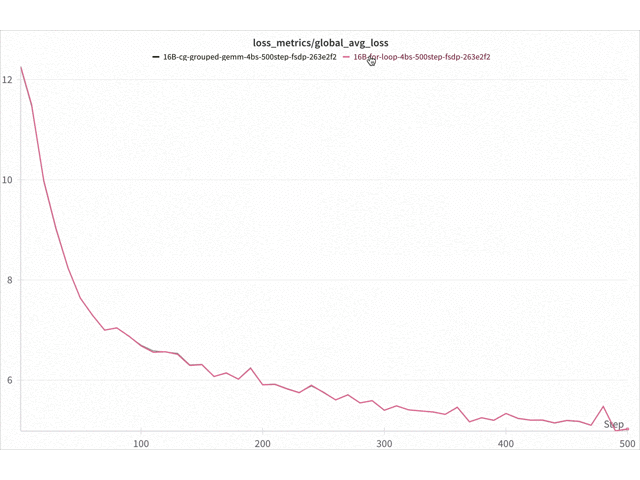
Figure 9. Loss curve comparison Triton vs for-loop 16B DeepSeekv3 on 8x NVIDIA H100 with FSDP2
Conclusion
For future work, we plan to integrate our kernel into vLLM (in-progress PR here), as well as extend this kernel to support FP8 in the forward and backward. Our kernel can be leveraged from torchtitan here. Further, we also plan to experiment with even lower precision datatypes such as MXFP4 that are supported by newer generation NVIDIA GPUs such as B200.
