Tokenization is a fundamental pre-processing step for most natural language processing (NLP) applications. It involves splitting text into smaller units called tokens (e.g., words or word segments) in order to turn an unstructured input string into a sequence of discrete elements that is suitable for a machine learning (ML) model. ln deep learning–based models (e.g., BERT), each token is mapped to an embedding vector to be fed into the model.
 |
| Tokenization in a typical deep learning model, like BERT. |
A fundamental tokenization approach is to break text into words. However, using this approach, words that are not included in the vocabulary are treated as “unknown”. Modern NLP models address this issue by tokenizing text into subword units, which often retain linguistic meaning (e.g., morphemes). So, even though a word may be unknown to the model, individual subword tokens may retain enough information for the model to infer the meaning to some extent. One such subword tokenization technique that is commonly used and can be applied to many other NLP models is called WordPiece. Given text, WordPiece first pre-tokenizes the text into words (by splitting on punctuation and whitespaces) and then tokenizes each word into subword units, called wordpieces.
 |
| The WordPiece tokenization process with an example sentence. |
In “Fast WordPiece Tokenization”, presented at EMNLP 2021, we developed an improved end-to-end WordPiece tokenization system that speeds up the tokenization process, reducing the overall model latency and saving computing resources. In comparison to traditional algorithms that have been used for decades, this approach reduces the complexity of the computation by an order of magnitude, resulting in significantly improved performance, up to 8x faster than standard approaches. The system has been applied successfully in a number of systems at Google and has been publicly released in TensorFlow Text.
Single-Word WordPiece Tokenization
WordPiece uses a greedy longest-match-first strategy to tokenize a single word — i.e., it iteratively picks the longest prefix of the remaining text that matches a word in the model’s vocabulary. This approach is known as maximum matching or MaxMatch, and has also been used for Chinese word segmentation since the 1980s. Yet despite its wide use in NLP for decades, it is still relatively computation intensive, with the commonly adopted MaxMatch approaches’ computation being quadratic with respect to the input word length (n). This is because two pointers are needed to scan over the input: one to mark a start position, and the other to search for the longest substring matching a vocabulary token at that position.
We propose an alternative to the MaxMatch algorithm for WordPiece tokenization, called LinMaxMatch, which has a tokenization time that is strictly linear with respect to n. First, we organize the vocabulary tokens in a trie (also called a prefix tree), where each trie edge is labeled by a character, and a tree path from the root to some node represents a prefix of some token in the vocabulary. In the figure below, nodes are depicted as circles and tree edges are black solid arrows. Given a trie, a vocabulary token can be located to match an input text by traversing from the root and following the trie edges to match the input character by character; this process is referred to as trie matching.
The figure below shows the trie created from the vocabulary consisting of “a”, “abcd”, “##b”, “##bc”, and “##z”. An input text “abcd” can be matched to a vocabulary token by walking from the root (upper left) and following the trie edges with labels “a”, “b”, “c”, “d” one by one. (The leading “##” symbols are special characters used in WordPiece tokenization that are described in more detail below.)
 |
| Trie diagram of the vocabulary [“a”, “abcd”, “##b”, “##bc”, “##z”]. Circles and arrows represent nodes and edges along the trie, respectively. |
Second, inspired by the Aho-Corasick algorithm, a classical string-searching algorithm invented in 1975, we introduce a method that breaks out of a trie branch that fails to match the given input and skips directly to an alternative branch to continue matching. As in standard trie matching, during tokenization, we follow the trie edges to match the input characters one by one. When trie matching cannot match an input character for a given node, a standard algorithm would backtrack to the last character where a token was matched and then restart the trie matching procedure from there, which results in repetitive and wasteful iterations. Instead of backtracking, our method triggers a failure transition, which is done in two steps: (1) it collects the precomputed tokens stored at that node, which we call failure pops; and (2) it then follows the precomputed failure link to a new node from which the trie matching process continues.
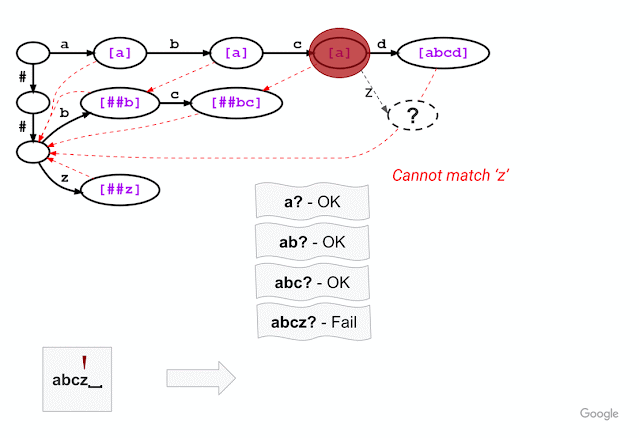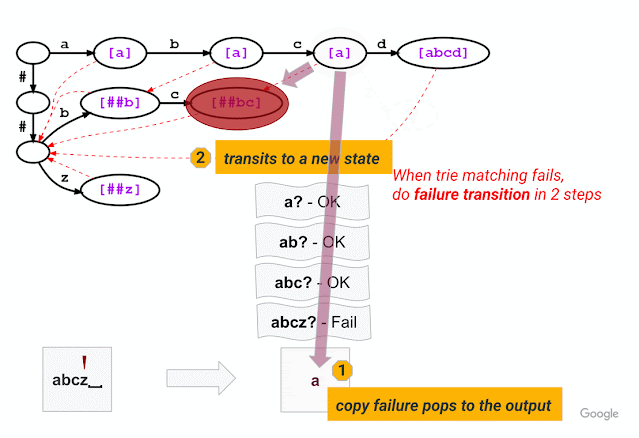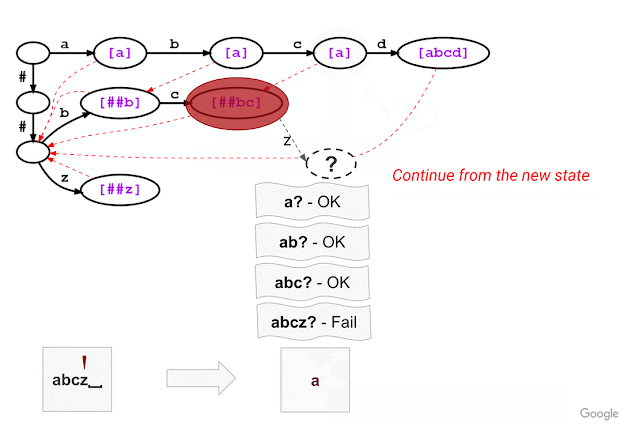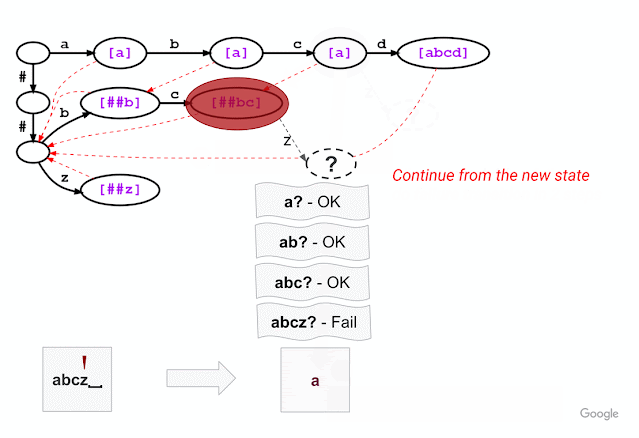
For example, given a model with the vocabulary described above (“a”, “abcd”, “##b”, “##bc”, and “##z”), WordPiece tokenization distinguishes subword tokens matching at the start of the input word from the subword tokens starting in the middle (the latter being marked with two leading hashes “##”). Hence, for input text “abcz”, the expected tokenization output is [“a”, “##bc”, “##z”], where “a” matches at the beginning of the input while “##bc” and “##z” match in the middle. For this example, the figure below shows that, after successfully matching three characters ‘a’, ‘b’, ‘c’, trie matching cannot match the next character ‘z’ because “abcz” is not in the vocabulary. In this situation, LinMaxMatch conducts a failure transition by outputting the first recognized token (using the failure pop token “a”) and following the failure link to a new node to continue the matching process (in this case, node with “##bc” as the failure pop tokens).The process then repeats from the new node.
Since at least n operations are required to read the entire input, the LinMaxMatch algorithm is asymptotically optimal for the MaxMatch problem.
End-to-End WordPiece Tokenization
Whereas the existing systems pre-tokenize the input text (splitting it into words by punctuation and whitespace characters) and then call WordPiece tokenization on each resulting word, we propose an end-to-end WordPiece tokenizer that combines pre-tokenization and WordPiece into a single, linear-time pass. It uses the LinMaxMatch trie matching and failure transitions as much as possible and only checks for punctuation and whitespace characters among the relatively few input characters that are not handled by the loop. It is more efficient as it traverses the input only once, performs fewer punctuation / whitespace checks, and skips the creation of intermediate words.
 |
| End-to-End WordPiece Tokenization. |
Benchmark Results
We benchmark our method against two widely-adopted WordPiece tokenization implementations, HuggingFace Tokenizers, from the HuggingFace Transformer library, one of the most popular open-source NLP tools, and TensorFlow Text, the official library of text utilities for TensorFlow. We use the WordPiece vocabulary released with the BERT-Base, Multilingual Cased model.
We compared our algorithms with HuggingFace and TensorFlow Text on a large corpus (several million words) and found that the way the strings are split into tokens is identical to other implementations for both single-word and end-to-end tokenization.
To generate the test data, we sample 1,000 sentences from the multilingual Wikipedia dataset, covering 82 languages. On average, each word has four characters, and each sentence has 82 characters or 17 words. We found this dataset large enough because a much larger dataset (consisting of hundreds of thousands of sentences) generated similar results.
We compare the average runtime when tokenizing a single word or general text (end-to-end) for each system. Fast WordPiece tokenizer is 8.2x faster than HuggingFace and 5.1x faster than TensorFlow Text, on average, for general text end-to-end tokenization.
 |
| Average runtime of each system. Note that for better visualization, single-word tokenization and end-to-end tokenization are shown in different scales. |
We also examine how the runtime grows with respect to the input length for single-word tokenization. Because of its linear-time complexity, the runtime of LinMaxMatch increases at most linearly with the input length, which is much slower than other quadratic-time approaches.
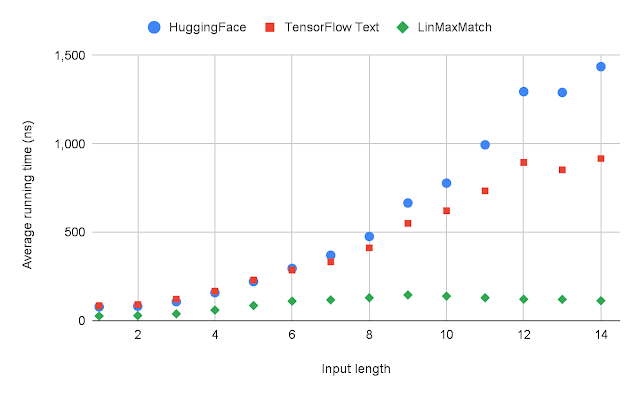 |
| The average runtime of each system with respect to the input length for single-word tokenization. |
Conclusion
We proposed LinMaxMatch for single-word WordPiece tokenization, which solves the decades-old MaxMatch problem in the asymptotically-optimal time with respect to the input length. LinMaxMatch extends the Aho-Corasick Algorithm, and the idea can be applied to more string search and transducer challenges. We also proposed an End-to-End WordPiece algorithm that combines pre-tokenization and WordPiece tokenization into a single, linear-time pass for even higher efficiency.
Acknowledgements
We gratefully acknowledge the key contributions and useful advices from other team members and colleagues, including Abbas Bazzi, Alexander Frömmgen, Alex Salcianu, Andrew Hilton, Bradley Green, Ed Chi, Chen Chen, Dave Dopson, Eric Lehman, Fangtao Li, Gabriel Schubiner, Gang Li, Greg Billock, Hong Wang, Jacob Devlin, Jayant Madhavan, JD Chen, Jifan Zhu, Jing Li, John Blitzer, Kirill Borozdin, Kristina Toutanova, Majid Hadian-Jazi, Mark Omernick, Max Gubin, Michael Fields, Michael Kwong, Namrata Godbole, Nathan Lintz, Pandu Nayak, Pew Putthividhya, Pranav Khaitan, Robby Neale, Ryan Doherty, Sameer Panwar, Sundeep Tirumalareddy, Terry Huang, Thomas Strohmann, Tim Herrmann, Tom Small, Tomer Shani, Wenwei Yu, Xiaoxue Zang, Xin Li, Yang Guo, Yang Song, Yiming Xiao, Yuan Shen, and many more.