Introduction
One of the tenets of modern neuroscience is that the brain modifies the
strengths of its synaptic connections (“weights”) during learning in
order to better adapt to its environment. However, the underlying
learning rules (“weight updates”) in the brain are currently unknown.
Many proposals have been suggested, ranging from Hebbian-style
mechanisms that seem biologically plausible but are not very effective
as learning algorithms in that they prescribe purely local changes to
the weights between two neurons that increase only if they activate
together — to backpropagation, which is effective from a learning
perspective by assigning credit to neurons along the entire downstream
path from outputs to inputs, but has numerous biologically implausible
elements.
A major long-term goal of computational neuroscience is to identify
which learning rules actually drive learning in the brain. A further
difficulty is that we do not even have strong ideas for what needs to be
measured in the brain to quantifiably assert that one learning rule is
more consistent with those measurements than another learning rule. So
how might we approach these issues? We take a simulation-based approach,
meaning that experiments are done on artificial neural networks rather
than real brains. We train over a thousand artificial neural networks
across a wide range of possible learning rule types (conceived of as
“optimizers”), system architectures, and tasks, where the ground truth
learning rule is known, and quantify the impact of these choices. Our
work suggests that recording activities from several hundred neurons,
measured semi-regularly during learning, may provide a good basis to
identify learning rules — a testable hypothesis within reach of
current neuroscience tools!
Background: A Plethora of Theories and a Paucity of Evidence
The brain modifies the connections between neurons during learning to
improve behavior; however, the underlying rules that govern these
modifications are unknown. The most famous proposed learning rule is
“Hebbian learning”, also known by the mantra: “neurons that fire
together; wire together”. In this proposal, a synaptic connection
strengthens if one neuron (“pre-synaptic”) consistently sends a signal
to another neuron (“post-synaptic”). The changes prescribed by Hebbian
learning are “local” in that they do not take into account a synapse’s
influence further downstream in the network. This locality makes
learning rather slow even in the cases where additional issues, such as
the weight changes becoming arbitrarily large, are mitigated. Though
there have been many suggested theoretical strategies to deal with this
problem, commonly involving simulations with artificial neural networks
(ANNs), these strategies appear difficult to scale up to solve
large-scale tasks such as ImageNet categorization
[1].
This property of local changes is in stark contrast to backpropagation,
the technique commonly used to optimize artificial neural networks. In
backpropagation, as the name might suggest, an error signal is
propagated backward along the entire downstream path from the outputs of
a model to the inputs of the model. This allows credit to be effectively
assigned to every neuron along the path.
Although backpropagation has long been a standard component of deep
learning, its plausibility as a biological learning rule (i.e. how the
brain modifies the strengths of its synaptic connections) is called into
question for several reasons. Chief among them is that backpropagation
requires perfect symmetry, whereby the backward error-propagating
weights are the transpose of the forward inference weights, for which
there is currently little biological support
[2,
3].
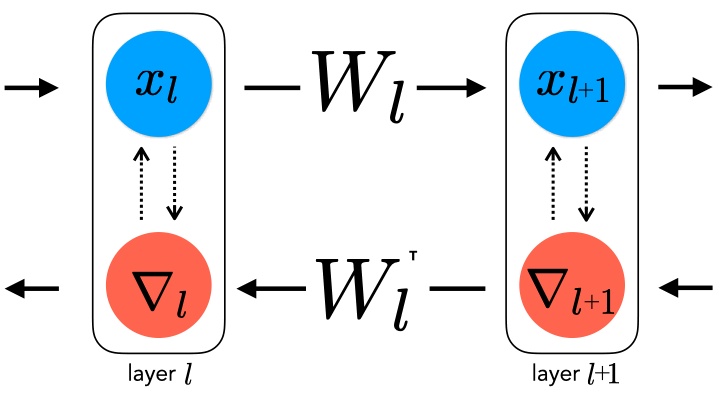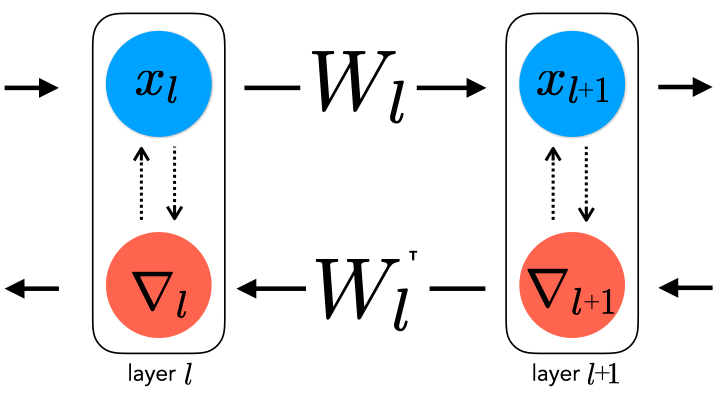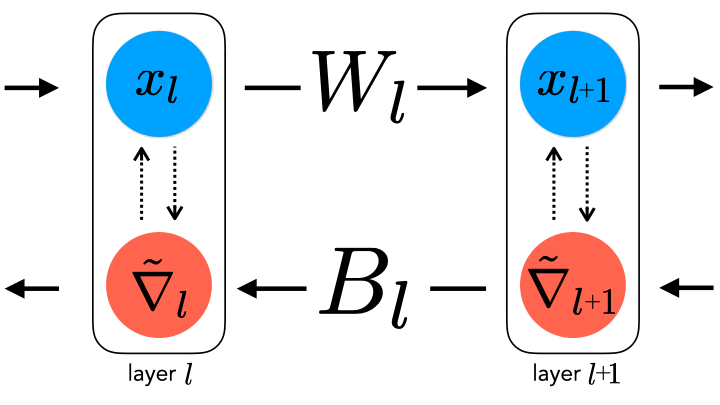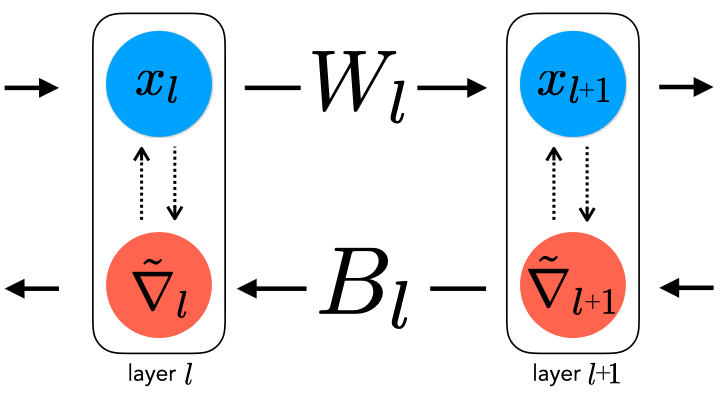
forward and backward weights. This constraint can be relaxed by
uncoupling them, thereby generating a spectrum of learning rule
hypotheses about how the backward weights may be updated.
For more details, see our recent prior work.
Recent approaches, from us and others
[4,
5], introduce approximate
backpropagation strategies that do not require this symmetry, and can
still succeed at large-scale learning as backpropagation does. However,
given the number of proposals, a natural question to ask is how
realistic they are. At the moment, our hypotheses are governed by domain
knowledge that specifies what “can” and “cannot” be biologically
plausible (e.g. “exact weight symmetry is likely not possible” or
“separate forward and backward passes during learning seem
implausible”), as well as characterizations of ANN task performance
under a given learning rule (which is not always directly measurable
from animal behavior). In order to be able to successfully answer this
question, we need to be able to empirically refute hypotheses. In
other words, we would ideally want to know what biological data to
collect in order to claim that one hypothesis is more likely than
another.
More concretely, we can ask: what specific measurements from the brain,
in the form of individual activation patterns over time, synaptic
strengths, or paired-neuron input-output relations, would allow one to
draw quantitative comparisons of whether the observations are more
consistent with one or another specific learning rule? For example,
suppose we record neural responses (“activation patterns”) while an
animal is learning a task. Would these data be sufficient to enable us
to broadly differentiate between learning rule hypotheses, e.g. by
reliably indicating that one learning rule’s changes over time more
closely match the changes measured from real data than those prescribed
by another learning rule?
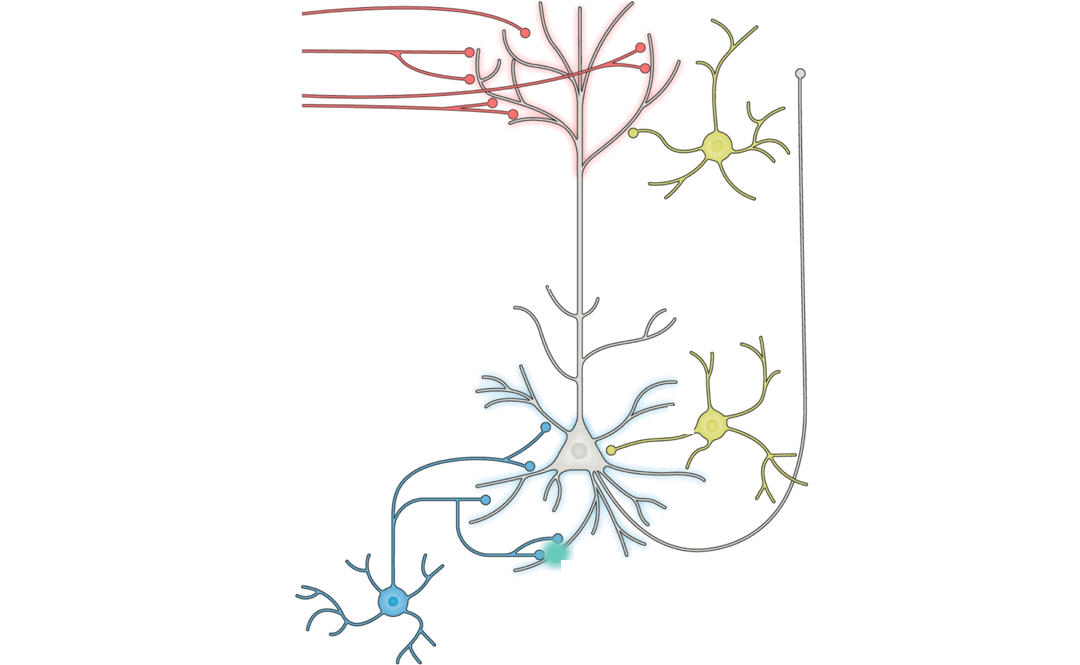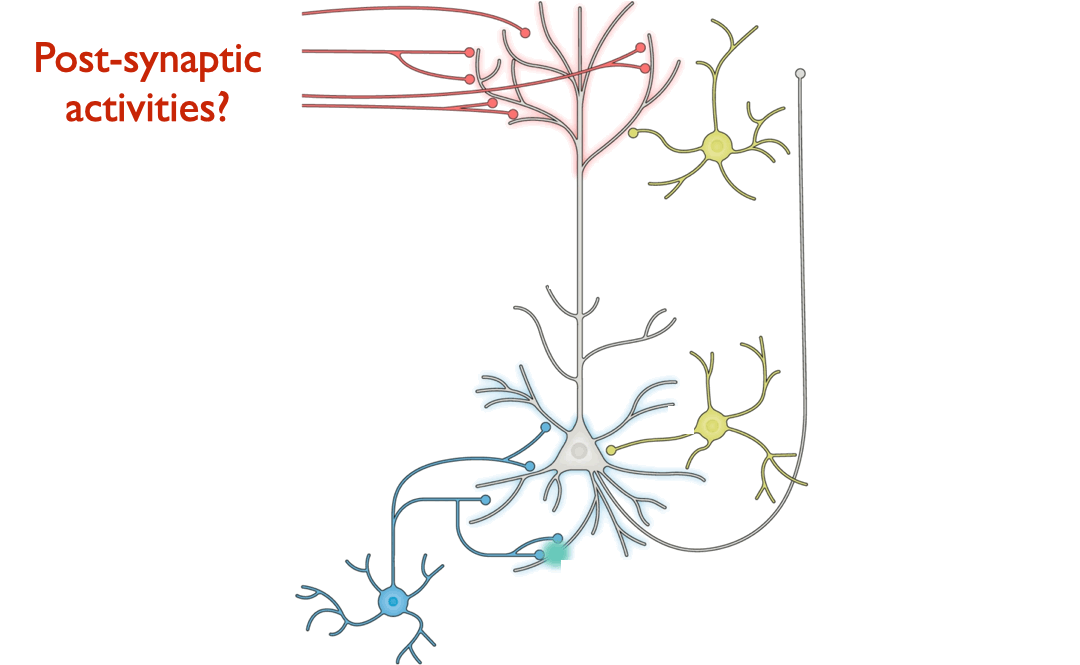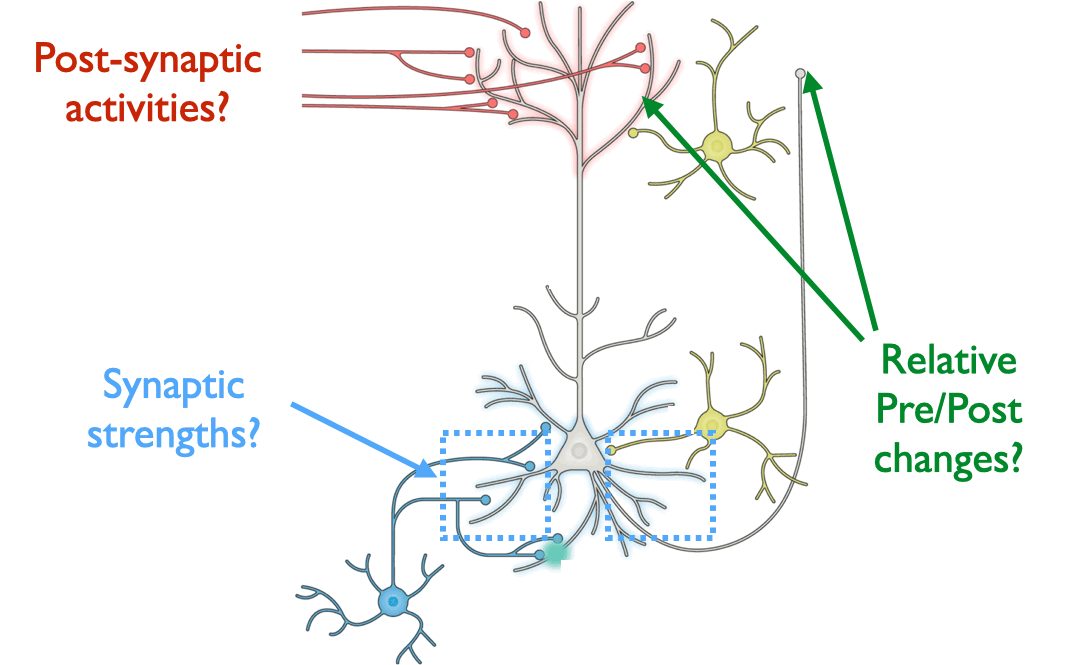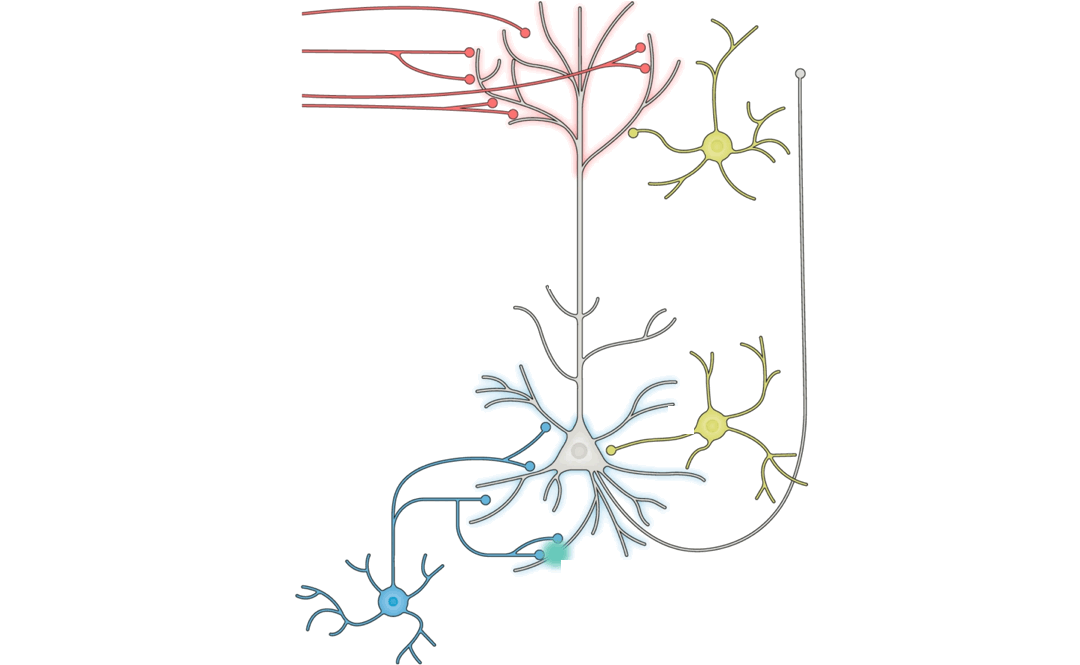
learning rule hypotheses. (Pyramidal neuron schematic adapted from Figure
4 of [6])
Answering this question turns out to be a substantial challenge, because
it is difficult on purely theoretical grounds to identify which patterns
of neural changes arise from given learning rules, without also knowing
the overall network connectivity and reward target (if any) of the
learning system.
But, there may be a silver lining. While ANNs consist of units that are
highly simplified with respect to biological neurons, recent progress
within the past few years has shown that the internal representations that
emerge in trained deep ANNs often overlap strongly with representations
in the brain, and are in fact quantifiably similar to many
neurophysiological and behavioral observations in animals
[7]. For
instance, task-optimized, deep convolutional neural networks (CNNs) have
emerged as quantitatively accurate models of encoding in primate visual
cortex [8,
9,
10]. This is
due to (1) their cortically-inspired architecture, a cascade of
spatially-tiled linear and nonlinear operations; and (2) their being
optimized to perform certain behaviors that animals must perform to
survive, such as object recognition
[11]. CNNs trained
to recognize objects on ImageNet predict neural responses of primate
visual cortical neurons better than any other model class. Thus, these
models are, at the moment, some of our current best algorithmic
“theories” of the brain — a system that was ultimately not designed by
us, but rather the product of millions of years of evolution. On the
other hand, ANNs are designed by us — so the ground truth learning
rule is known and every unit (artificial “neuron”) can be measured up to
machine precision.
Can we marry what we can measure in neuroscience with what we can
conclude from machine learning, in order to identify what experimentally
measurable observables may be most useful for inferring the underlying
learning rule? If we can’t do this in our models, then it seems very
unlikely to be able to do this in the real brain. But if we can do this
in principle, then we are in a position to generate predictions as to
what data to collect, and whether that is even within reach of current
experimental neuroscience tools.
Methods
We adopt a two-stage “virtual experimental” approach. In the first
stage, we train ANNs with different learning rules, across a variety of
architectures, tasks, and associated hyperparameters. These will serve
as our “model organisms” on which we will subsequently perform idealized
neuroscience measurements. In the second stage, we calculate aggregated
statistics (“measurements”) from each layer of the models as features
from which to train simple classifiers that classify the category that a
given learning rule belongs to (specified below). These classifiers
include the likes of a linear SVM, as well as simple non-linear ones
such as a Random Forest and a 1D convolutional two-layer perceptron.
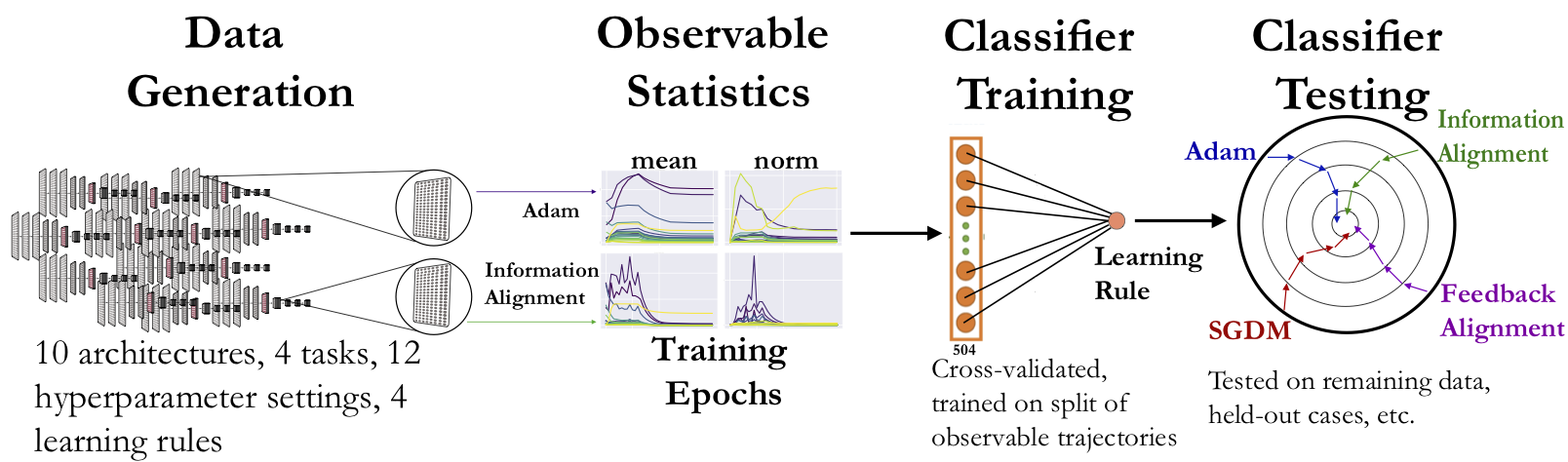
neural network’s layer, through the model training process for each
learning rule. We take a quantitative approach whereby a classifier is
cross-validated and trained on a subset of these trajectories and
evaluated on the remaining data.
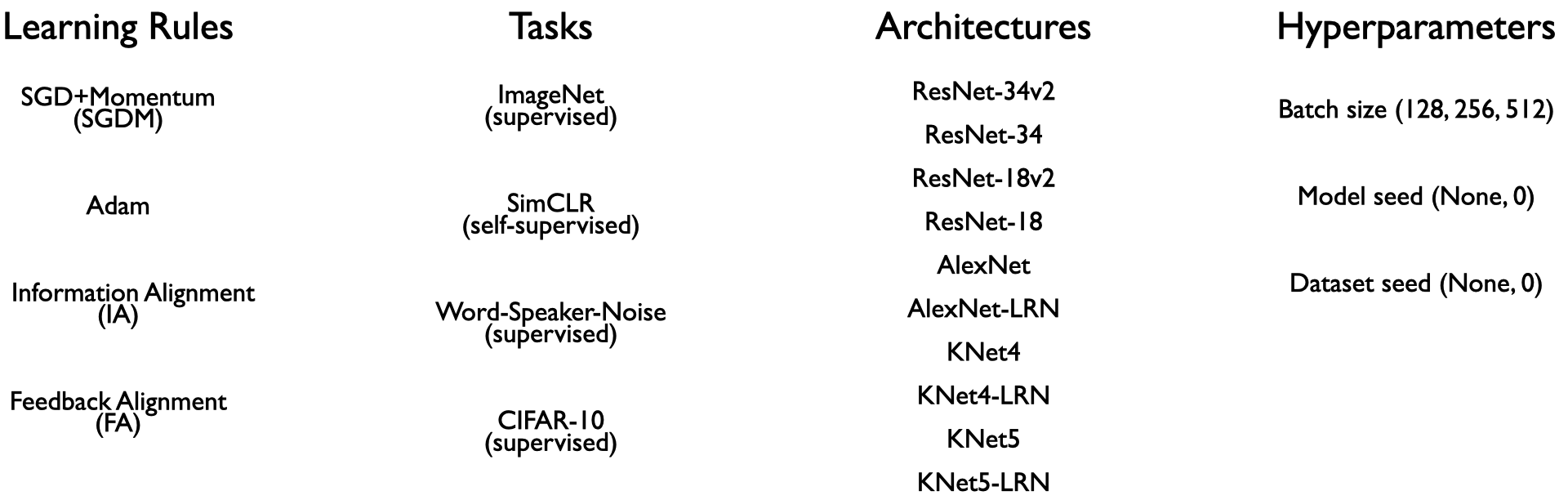
Generating a large-scale dataset is crucial to this endeavor, in order
to both emulate a variety of experimental neuroscience scenarios and be
able to derive robust conclusions from them. Thus, in the first stage,
we train ANNs on tasks and architectures that have been shown to explain
variance in neural responses from sensory (visual and auditory)
brain areas [8,
12].
These include supervised tasks across vision and audition, as well as
self-supervised ones. We consider both shallow and deep feedforward
architectures on these tasks, that are of depth comparable to what is
considered reasonable from the standpoint of shallower non-primate (e.g.
mouse
[13]) and
deeper primate sensory systems
[8,
14,
15].
we generate data, comprising over a thousand training experiments in total.
In the second stage, we train classifiers on the observable statistics from these ANNs to predict the learning rules (as specified in the table above) used to train them.
The four learning rules were chosen as they span the space of commonly
used variants of backpropagation (SGDM and Adam), as well as potentially
more biologically-plausible “local” learning rules (Feedback
Alignment (FA) and Information Alignment (IA)) that efficiently
train networks at scale to varying degrees of performance but avoid exact weight
symmetry.
Because the primary aim of this study is to determine the extent that
different learning rules led to different encodings within ANNs, we
begin by defining representative features that can be drawn from the
course of model training. For each layer in a model, we consider three
measurements: weights of the layer, activations from the layer, and
layer-wise activity change of a given layer’s outputs relative to its
inputs. We choose ANN weights to analogize to synaptic strengths in the
brain, activations to analogize to post-synaptic firing rates, and
layer-wise activity changes to analogize to paired measurements that
involve observing the change in post-synaptic activity with respect to
changes induced by pre-synaptic input.

For each measure, we consider three functions applied to it: “identity”,
“absolute value”, and “square”. Finally, for each function of the
weights and activations, we consider seven statistics, and for the
layer-wise activity change observable, we only use the mean statistic
due to computational restrictions. This results in a total of 45
continuous valued observable statistics for each layer, though 24
observable statistics are ultimately used for training the classifiers,
since we remove any statistic that has a divergent value during the
course of model training. We also use a ternary indicator of layer
position in the model hierarchy: “early”, “middle”, or “deep”
(represented as a one-hot categorical variable).
We Can Separate Learning Rules from Aggregate Statistics of the Weights, Activations, or Layer-wise Activity Changes
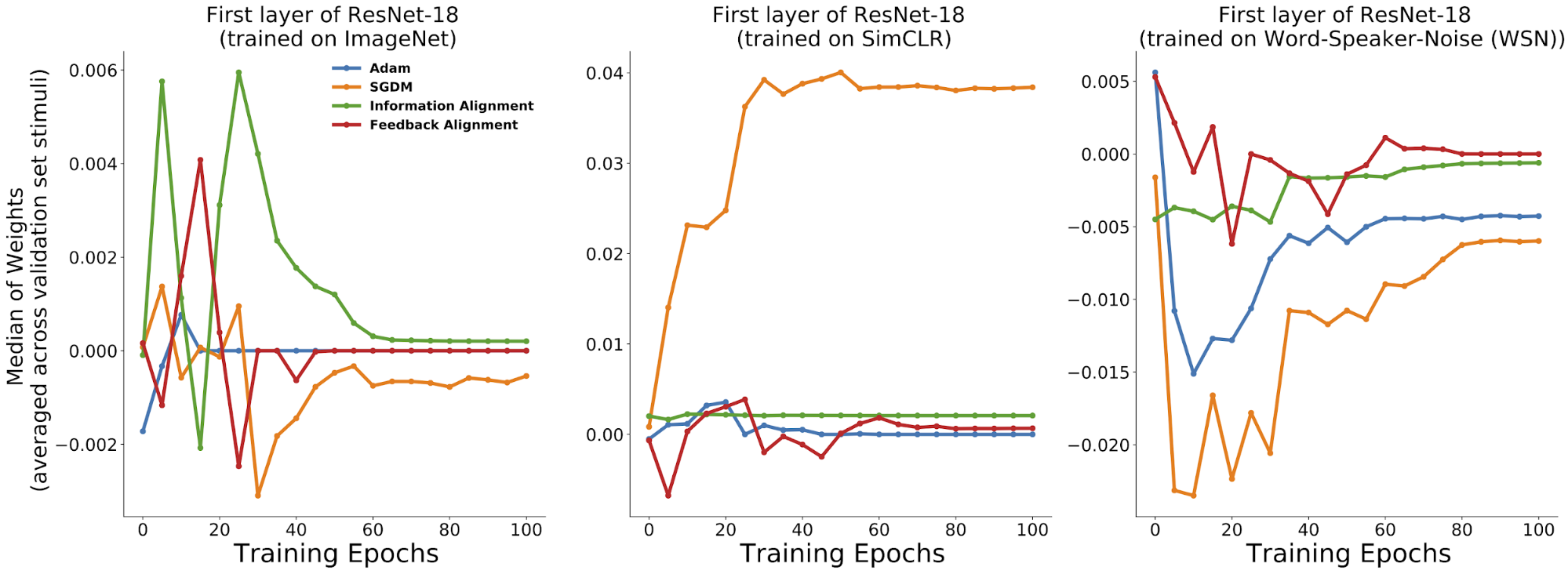
differences in observable statistics.
Already by eye, one can pick up distinctive differences across the
learning rules for each of the training trajectories of these metrics.
Of course, this is not systematic enough to clearly judge one set of
observables versus another, but provides some initial assurance that
these metrics seem to capture some inherent differences in learning
dynamics across rules.
So these initial observations seem promising, but we want to make this
approach more quantitative. Suppose for each layer we concatenate the
trajectories of each observable and the position in the model hierarchy
that this observable came from. Can we generalize well across held-out
examples?
It turns out that the answer is in fact, yes. Across all classes of
observables, the Random Forest attains the highest test accuracy, and
all observable measures perform similarly under this classifier.
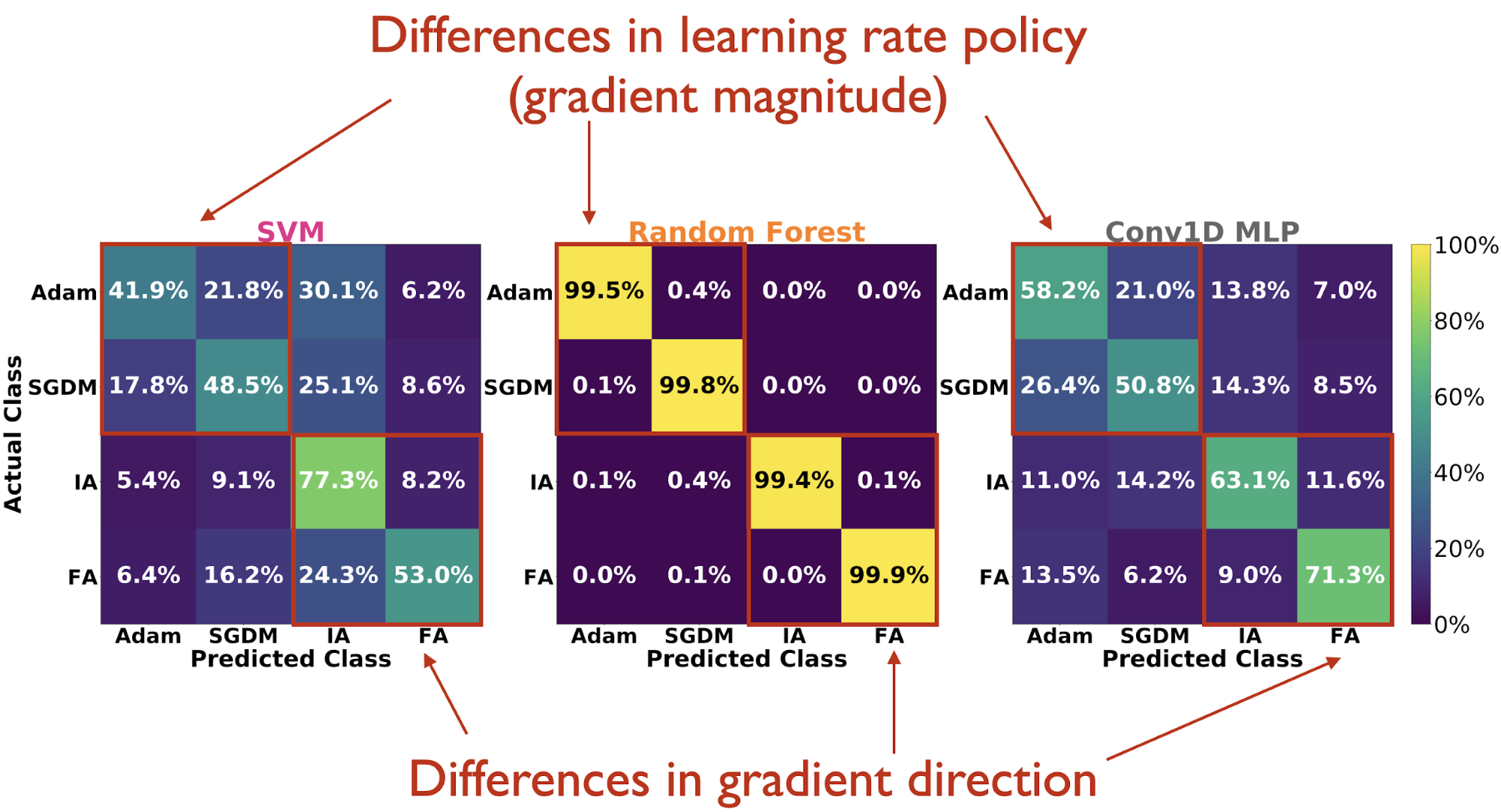
(Adam vs. SGDM) are more difficult to distinguish.
Looking at confusion matrices on the test set, we see that the Random
Forest hardly mistakes one learning rule from any of the others. And
when the classifiers do make mistakes, they generally tend to confuse
Adam vs. SGDM more so than IA vs. FA, suggesting that they are able to
pick up more on differences (reflected in the observable statistics) due
to high-dimensional direction of the gradient tensor than the magnitude
of the gradient tensor (the latter being directly tied to learning rate
policy).
Adding Back Some Experimental Neuroscience Realism
Up until this point, we have had access to all input types, the full learning trajectory, and noiseless access to all units when making our virtual measurements of ANN observable statistics.
But in a real experiment where someone were to
collect such data from a neural circuit, the situation would be far from
this ideal scenario. We therefore explore experimental realism in
several ways, in order to identify which observable measures are robust
across these scenarios.
Access to only portions of the learning trajectory: subsampling observable trajectories
The results presented thus far were obtained with access to the entire
learning trajectory of each model. Often however, an experimentalist
collects data throughout learning at regularly spaced intervals. We
capture this variability by randomly sampling a fixed number of points
at a fixed temporal spacing for each trajectory, which we refer to as a
“subsample period”.
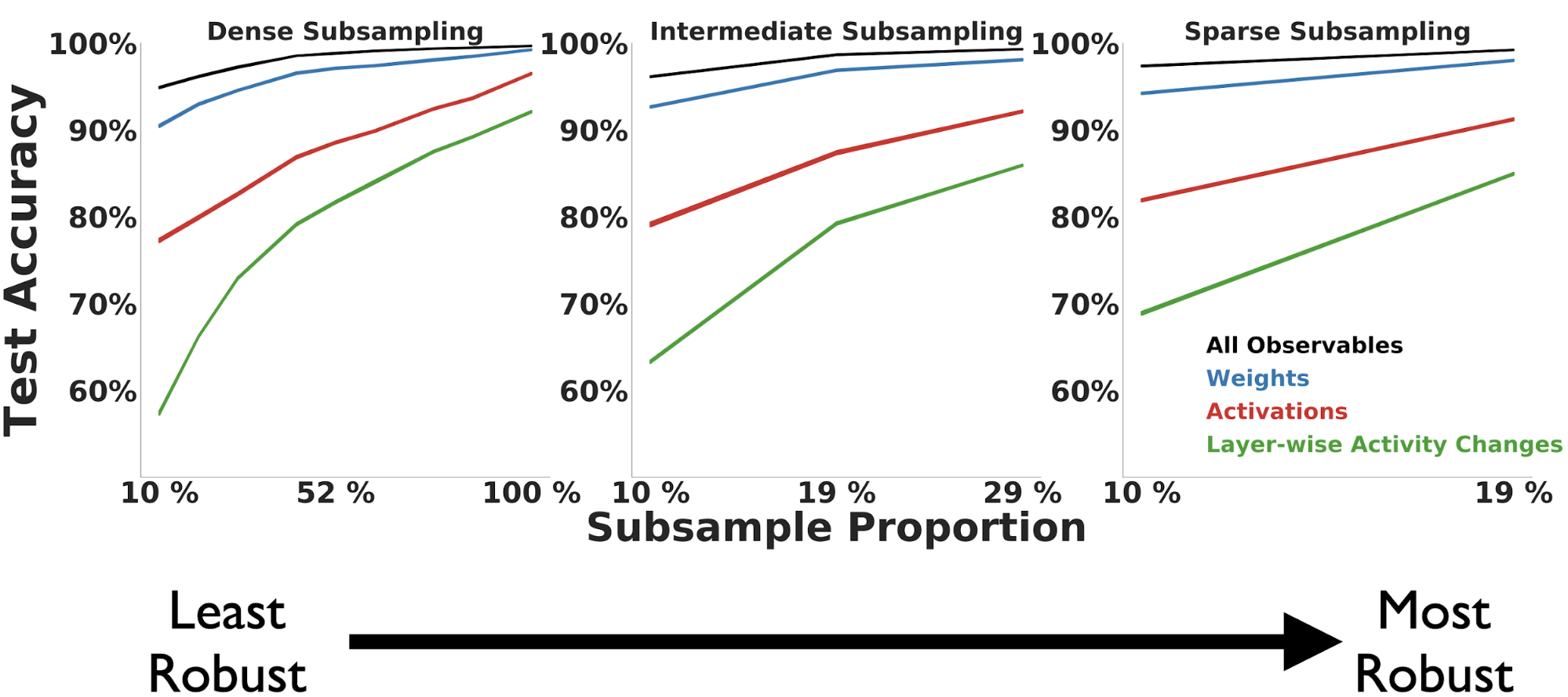
trajectory undersampling.
We find across observable measures that robustness to undersampling of
the trajectory is largely dependent on the subsample period length. As
the subsample period length increases (in the middle and right-most
columns), the Random Forest classification performance increases
compared to the same number of sampled points for a smaller period
(depicted in the left-most column).
Taken together, these results suggest that data consisting of
measurements collected temporally further apart across the learning
trajectory is more robust to undersampling than data collected closer
together in training time. Furthermore, across individual observable
measures, the weights are overall the most robust to undersampling of
the trajectory, but with enough frequency of samples we can achieve
comparable performance with the activations.
Incomplete and noisy measurements: subsampling units and Gaussian noise before collecting observables
The aggregate statistics computed from the observable measures thus far
have operated under the idealistic assumption of noiseless access to
every unit in the model. However, in most datasets, there is a
significant amount of unit undersampling as well as non-zero measurement
noise. How do these two factors affect learning rule identification, and
in particular, how noise and subsample-robust are particular observable
measures?
Addressing this question would provide insight into the types of
experimental neuroscience paradigms that may be most useful for
identifying learning rules, and predict how certain experimental tools
may fall short for given observables. For instance, optical imaging
techniques can use fluorescent indicators of electrical activities of
neurons to give us simultaneous access to thousands of neurons.
But these techniques can have lower temporal resolution and signal-to-noise than
electrophysiological recordings that more directly measure the
electrical activities of neurons, which in turn may lack the same
coverage.
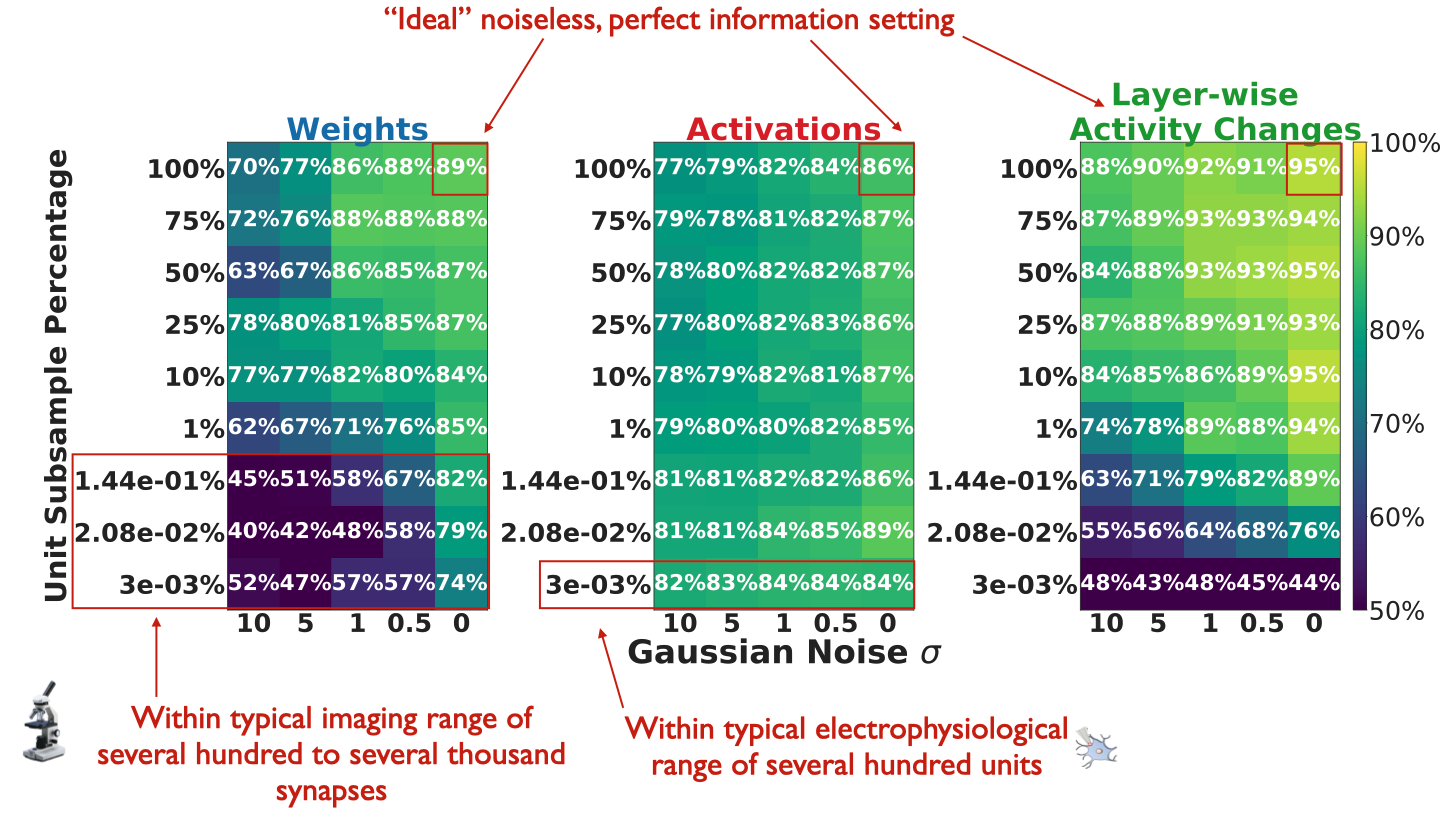
undersampling. Reported here is Random Forest test set accuracy in
separating IA vs. FA, averaged over 10 train/test splits per random
sampling and simulated measurement noise seed.
To account for these tradeoffs, we model measurement noise as an
additive white Gaussian noise process added to units of ResNet-18
trained on the ImageNet and self-supervised SimCLR tasks. We choose IA
vs. FA since the differences between them are conceptually stark: IA
imposes dynamics on the feedback error weights during learning, whereas
FA keeps them fixed. If there are scenarios of measurement noise and
unit subsampling where we are at chance accuracy for this problem (50%),
then it may establish a strong constraint on learning rule
separability more generally.
Our results suggest that if one makes experimental measurements by
imaging synaptic strengths, it is still crucial that the optical imaging
readout not be very noisy, since even with the amount of units typically
recorded currently (on the order of several hundred to several thousand
synapses), a noisy imaging strategy of synaptic strengths may be
rendered ineffective.
Instead, current electrophysiological techniques that measure the
activities from hundreds of units could form a good set of neural data
to separate learning rules. Recording more units with these techniques
can improve learning rule separability from the activities, but it does
not seem necessary, at least in this setting, to record a majority of
units to perform this separation effectively.
Conclusions
As experimental techniques in neuroscience continue to advance, we will
be able to record data from more neurons with higher temporal
resolution. But even if we had the perfect measurement tools, it is not
clear ahead of time what should be measured in order to identify the
learning rule(s) operative within a given neural circuit, or whether
this is even possible in principle. Our model-based approach
demonstrates that we can identify learning rules solely on the basis of
standard types of experimental neuroscience measurements from the
weights, activations, or layer-wise activity changes, without knowledge
of the architecture or loss target of the learning system.
Additionally, our results suggest the following prescription for the type of
experimental neuroscience data to be collected towards this goal:
Electrophysiological recordings of post-synaptic activities
from a neural circuit on the order of several hundred units, frequently
measured at wider intervals during the course of learning, may provide a
good basis on which to identify learning rules.
We have made our dataset, code, and interactive
tutorial publicly
available so that others can analyze these properties without needing to
train neural networks themselves. Our dataset may also be of interest to
researchers theoretically or empirically investigating learning in deep
neural networks. For further details, check out our NeurIPS 2020
paper.
Acknowledgements
I would like to thank my collaborator Sanjana Srivastava
and advisors Surya Ganguli and Daniel Yamins. I would also like to
thank Jacob Schreiber, Sidd Karamcheti, and Andrey Kurenkov for their
editorial suggestions on this post.
