Posted by Hsin-Yuan Huang, Google/Caltech, Michael Broughton, Google, Jarrod R. McClean, Google, Masoud Mohseni, Google.
Data drives machine learning. Large scale research and production ML both depend on high volume and high quality sources of data where it is often the case that more is better. The use of training data has enabled machine learning algorithms to achieve better performance than traditional algorithms at recognizing photos, understanding human languages, or even tasks that have been championed as premier applications for quantum computers such as predicting properties of novel molecules for drug discovery and the design of better catalysts, batteries, or OLEDs. Without data, these machine learning algorithms would not be any more useful than traditional algorithms.
While existing machine learning models run on classical computers, quantum computers provide the potential to design quantum machine learning algorithms that achieve even better performance, especially for modelling quantum-mechanical systems like molecules, catalysts, or high-temperature superconductors. Because the quantum world allows the superposition of exponentially many states to evolve and interfere at the same time while classical computers struggle at such tasks, one would expect quantum computers to have an advantage in machine learning problems that have a quantum origin. The hope is that such quantum advantage (the advantage of using quantum computers instead of classical computers) extends to machine learning problems in the classical domain, like computer vision or natural language processing.
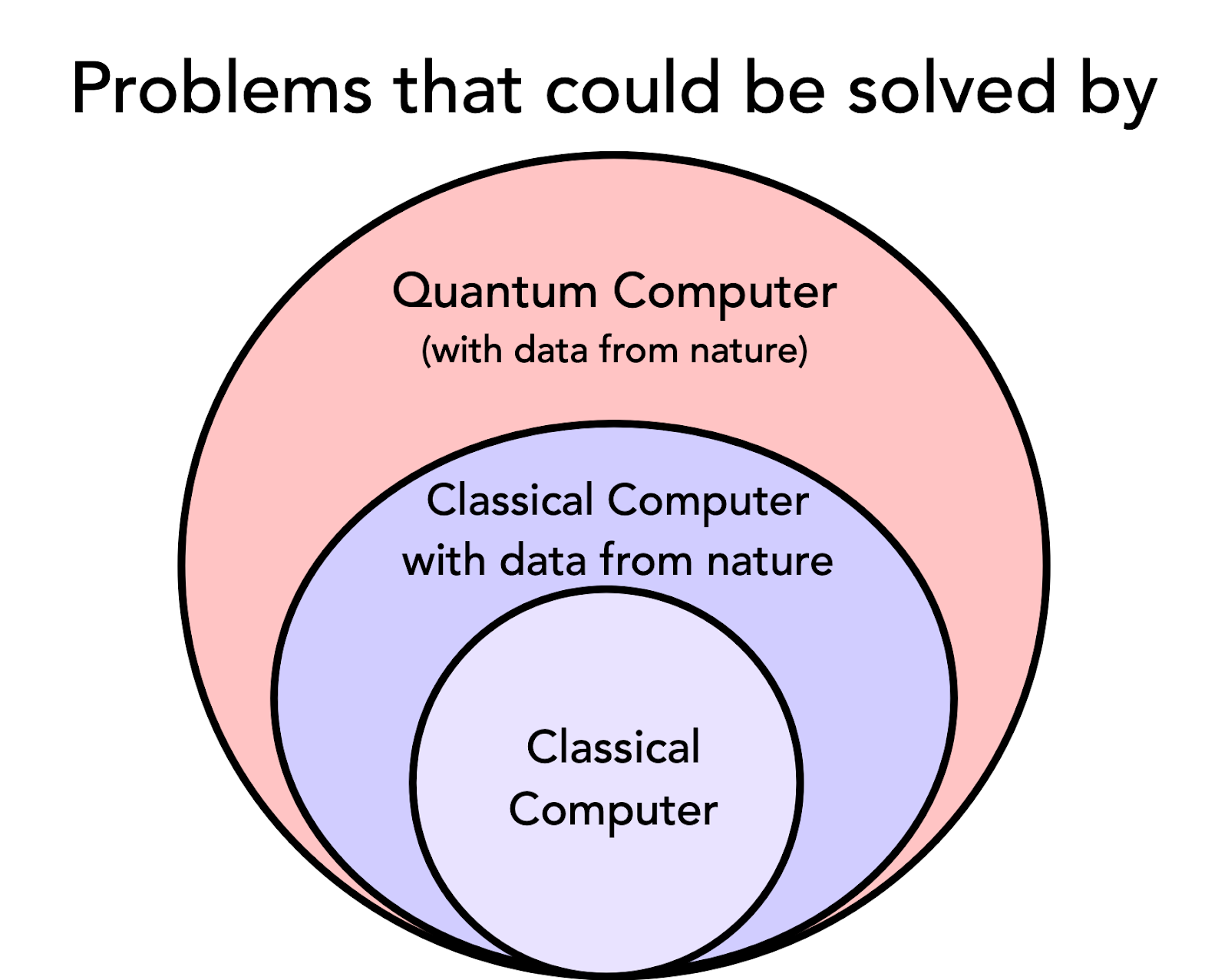
Learning from data obtained in nature (e.g., physical experiments) can enable classical computers to solve some problems that are hard for classical computers without the data. However, an even larger class of problems can be solved using quantum computers. If we assume nature can be simulated using quantum computers, then quantum computers with data obtained in nature will not have further computational power.
To understand the advantage of quantum computers in machine learning problems, the following big questions come to mind:
- If data comes from a quantum origin, such as from experiments developing new materials, are quantum models always better at predicting than classical models?
- Can we evaluate when there is a potential for a quantum computer to be helpful for modelling a given data set, from either a classical or quantum origin?
- Is it possible to find or construct a data set where quantum models have an advantage over their classical counterparts?
We addressed these questions and more in a recent paper by developing a mathematical framework to compare classical modelling approaches (neural networks, tree-based models, etc) against quantum modelling approaches in order to understand potential advantages in making more accurate predictions. This framework is applicable both when the data comes from the classical world (MNIST, product reviews, etc) and when the data comes from a quantum experiment (chemical reaction, quantum sensors, etc).
Conventional wisdom might suggest that the use of data coming from quantum experiments that are hard to reproduce classically would imply the potential for a quantum advantage. However, we show that this is not always the case. It is perhaps no surprise to machine learning experts that with enough data, an arbitrary function can be learned. It turns out that this extends to learning functions that have a quantum origin, too. By taking data from physical experiments obtained in nature, such as experiments for exploring new catalysts, superconductors, or pharmaceuticals, classical ML models can achieve some degree of generalization beyond the training data. This allows classical algorithms with data to solve problems that would be hard to solve using classical algorithms without access to the data (rigorous justification of this claim is given in our paper).
We provide a method to quantitatively determine the amount of samples required to make accurate predictions in datasets coming from a quantum origin. Perhaps surprisingly, sometimes there is no great difference between the number of samples needed by classical and quantum models. This method also provides a constructive approach to generate datasets that are hard to learn with some classical models.
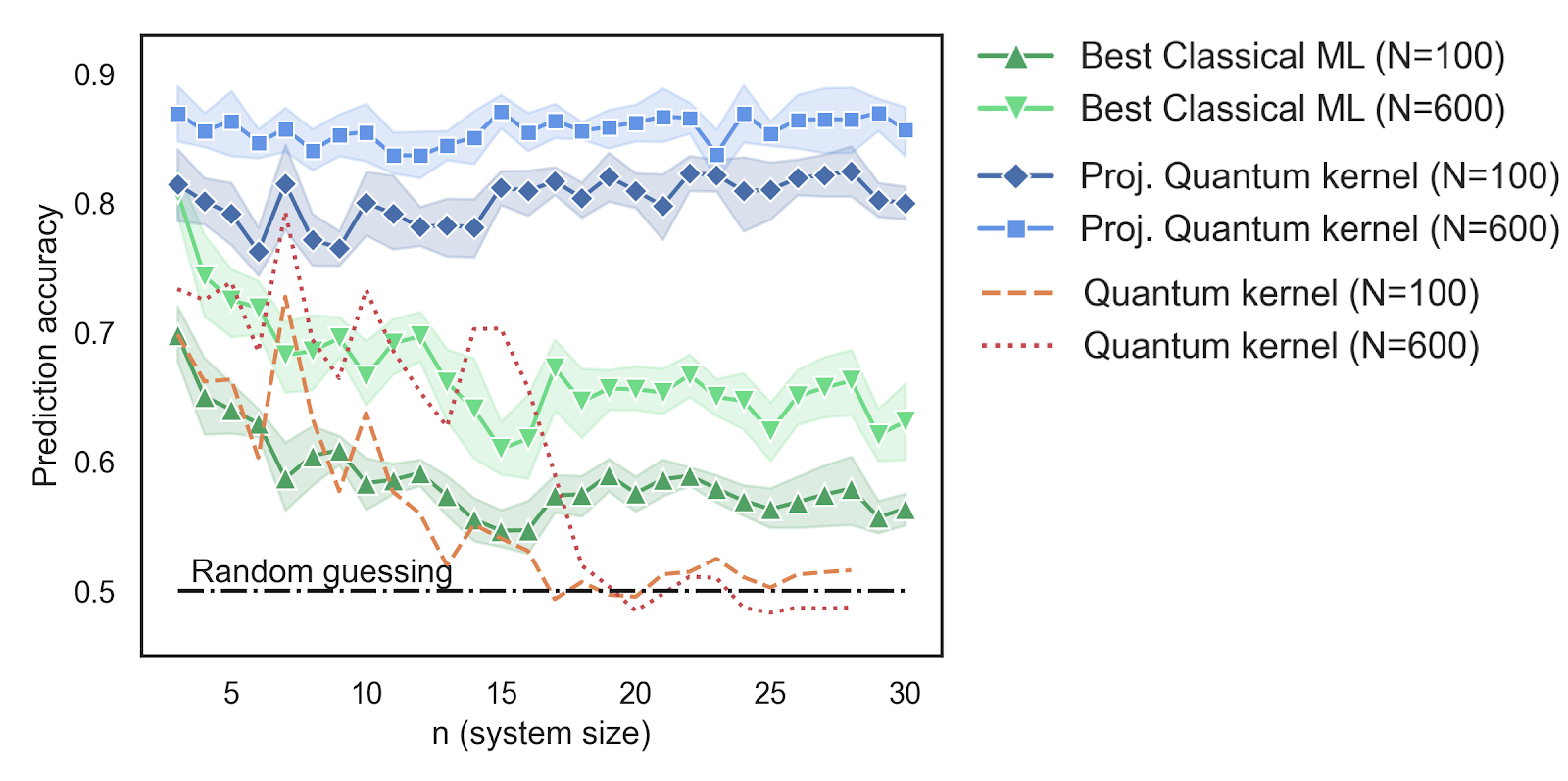
An empirical demonstration of prediction advantage using quantum models compared to the best among a list of common classical models under different amounts of training data N. The projected quantum kernel we introduce has a significant advantage over the best tested Classical ML.
We go on to use this framework to engineer datasets for which all attempted traditional machine learning methods fail, but quantum methods do not. An example of one such data set is presented in the above figure. These trends are examined empirically in the largest gate-based quantum machine learning simulations to date, made possible with TensorFlow Quantum, which is an open source library for quantum machine learning. In order to carry out this work at large quantum system sizes a considerable amount of computing power was needed. The combination of quantum circuit simulation (~300 TeraFLOP/s) and analysis code (~800 TeraFLOP/s) written using TensorFlow and TensorFlow Quantum was able to easily reach throughputs as high as 1.1 PetaFLOP/s, a scale that is rarely seen in the crossover field of quantum computing and machine learning (Though it is nothing new for classical ML which has already hit the exaflop scale).
When preparing distributed workloads for quantum machine learning research in TensorFlow Quantum, the setup and infrastructure should feel very familiar to regular TensorFlow. One way to handle distribution in TensorFlow is with the tf.distribute module, which allows users to configure device placement as well as machine configuration in multi-machine workloads. In this work tf.distribute was used to distribute workloads across ~30 Google cloud machines (some containing GPUs) managed by Kubernetes. The major stages of development were:
- Develop a functioning single-node prototype using TensorFlow and TensorFlow Quantum.
- Incorporate minimal code changes to use MultiWorkerMirroredStrategy in a manually configured two-node environment.
- Create a docker image with the functioning code from step 2. and upload it to the Google container registry .
- Using the Google Kubernetes engine, launch a job following along with the ecosystem templates provided here .
TensorFlow Quantum has a tutorial showcasing a variation of step 1. where you can create a dataset (in simulation) that is out of reach for classical neural networks.
It is our hope that the framework and tools outlined here help to enable the TensorFlow community to explore precursors of datasets that require quantum computers to make accurate predictions. If you want to get started with quantum machine learning, check out the beginner tutorials on the TensorFlow Quantum website. If you are a quantum machine learning researcher, you can read our paper addressing the power of data in quantum machine learning for more detailed information. We are excited to see what other kinds of large scale QML experiments can be carried out by the community using TensorFlow Quantum. Only through expanding the community of researchers will machine learning with quantum computers reach its full potential.