How heavy is an elephant? How expensive is a wedding ring?
Humans have a pretty good sense of scale, or reasonable ranges of these
numeric attributes, of different objects, but do pre-trained language
representations? Although pre-trained Language Models (LMs) like
BERT have
shown a remarkable ability to learn all kinds of knowledge, including
factual
knowledge,
it remains unclear whether their representations can capture these types
of numeric attributes from text alone without explicit training data.
In our recent
paper,
we measure the amount of scale information that is captured in several
kinds of pre-trained text representations and show that, although
generally a significant amount of such information is captured, there is
still a large gap between their current performance and the theoretical
upper bound. We identify that specifically those text representations
that are contextual and good at numerical reasoning capture scale
better. We also come up with a new version of BERT, called NumBERT, with
improved numerical reasoning by replacing numbers in the pretraining
text corpus with their scientific notation, which more readily exposes
the magnitude to the model, and demonstrate that NumBERT representations
capture scale significantly better than all those previous text
representations.
Scalar Probing
In order to understand to what extent pre-trained text representations, like
BERT representations, capture scale information, we propose a task
called scalar probing: probing the ability to predict a
distribution over values of a scalar attribute of an object. In this
work, we focus specifically on three kinds of scalar attributes: weight,
length, and price.
Here is the basic architecture of our scalar probing task:
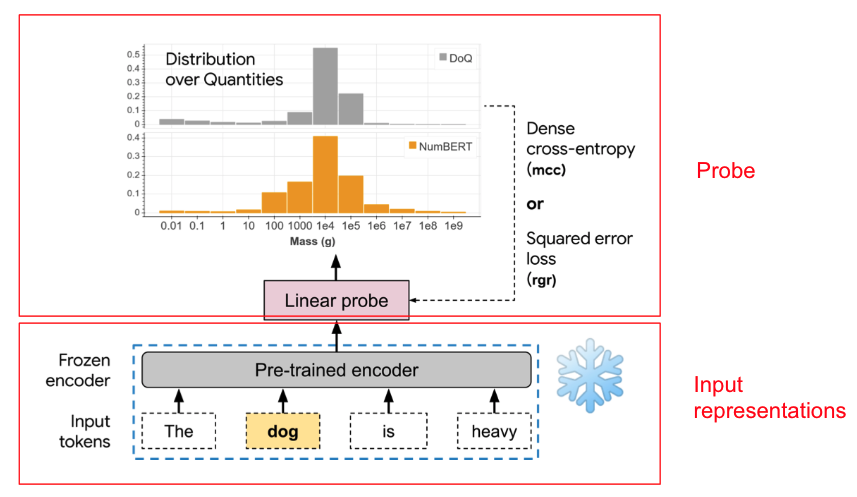
In this example, we are trying to see whether the representation of
“dog” extracted by a pre-trained encoder can be used to predict/recover
the distribution of the weight of a dog through a linear model. We probe
three baseline language representations:
Word2vec,
ELMo,
and
BERT.
Since the latter two are contextual representations that operate on
sentences instead of words, we feed in sentences constructed using fixed
templates. For example, for weight, we use the template “The X is
heavy”, where X is the object in interest.
We explore the kind of probe that predicts a point estimate of the value
and the kind that predicts the full distribution. For predicting a point
estimate, we use a standard linear ReGRession (we denote as “rgr”)
trained to predict the log of the median of all values for each object
for the scale attribute under consideration. We predict the log because,
again, we care about the general scale rather than the exact value. The
loss is calculated using the prediction and the log of the median of the
ground-truth distribution. For predicting the full distribution, we use
a linear softmax Multi-Class Classifier (we denote as “mcc”) producing a
categorical distribution over the 12 orders of magnitude. The
categorical distribution predicted using the NumBERT (our improved
version of BERT; will be introduced later) representations is shown as
the orange histogram in the above example.
The ground-truth distributions we use come from the Distributions over
Quantities (DoQ)
dataset which consists of empirical counts of scalar attribute values
associated with >350K nouns, adjectives, and verbs over 10 different
attributes, automatically extracted from a large web text corpus. Note
that during the construction of the dataset, all units for a certain
attribute are first unified to a single one (e.g.
centimeter/meter/kilometer -> meter) and the numeric values are scaled
accordingly. We convert the collected counts for each object-attribute
pair in DoQ into a categorical distribution over 12 orders of magnitude.
In the above example of the weight of a dog, the ground-truth
distribution is shown as the grey histogram, which is concentrated
around 10-100kg.
The better the predictive performance is across all the object-attribute
pairs we are dealing with, the better the pre-trained representations
encode the corresponding scale information.
NumBERT
Before looking at the scalar probing results of these different language
presentations, let’s also think about what kind of representations might
be good at capturing scale information and how to improve existing LMs
to capture scale better. All of these models are trained using large
online text corpora like Wikipedia, news, etc. How can their
representations pick up scale information from all this text?
Here is a piece of text from the first document I got when I searched on
Google “elephant weight”:
“…African elephants can range from 5,000 pounds to more than 14,000 pounds (6,350 kilograms)…”
So it is highly likely that the learning of scale is partly mediated by
the transfer of scale information from the numbers (here “5,000”,
“14,000”, etc.) to nouns (here “elephants”) and numeracy, i.e. the
ability to reason about numbers, is probably important for representing
scale!
However, previous
work has
shown that existing pre-trained text representations, including BERT,
ELMo, and Word2Vec, are not good at reasoning over numbers. For example,
beyond the magnitude of ~500, they cannot even decode a number from its
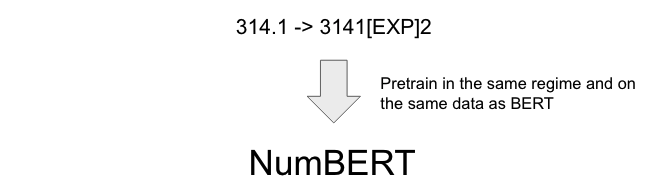
word embedding, e.g. embedding(“710”) 710. Thus, we propose to improve
the numerical reasoning abilities of these representations by replacing
every instance of a number in the LM training data with its scientific
notation, and re-pretraining BERT (which we call NumBERT). This enables
the model to more easily associate objects in the sentence directly with
the magnitude expressed in the exponent, ignoring the relatively
insignificant mantissa.
Results
Scalar Probing
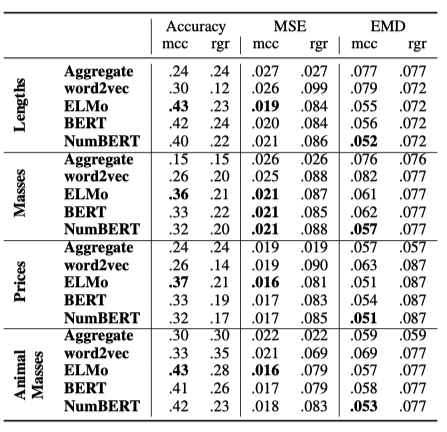
The above table shows the results of scalar probing on the DoQ data. We
use three evaluation metrics: Accuracy, Mean Squared Error (MSE), and
Earth Mover’s distance (EMD), and we do the experiments in four domains:
Lengths, Masses, Prices and Animal Masses (a subset of Masses). For MSE
and EMD, the best possible score is 0, while we compute a loose upper
bound of accuracy by sampling from the ground-truth distribution and
evaluating against the mode. This upper bound achieves accuracies of
0.570 for lengths, 0.537 for masses, and 0.476 for prices.
For the Aggregate baseline, for each attribute, we compute the empirical
distribution over buckets across all objects in the training set, and
use that as the predicted distribution for all objects in the test set.
Compared with this baseline, we can see that the mcc probe over the best
text representations capture about half (as measured by accuracy) to a
third (by MSE and EMD) of the distance to the upper bound mentioned
above, suggesting that while a significant amount of scalar information
is available, there is a long way to go to support robust commonsense
reasoning.
Specifically, NumBERT representations do consistently better than all
the others on Earth Mover’s Distance (EMD), which is the most
robust metric because of its better convergence
properties and
robustness to adversarial perturbations of the data
distribution. Word2Vec
performs significantly worse than the contextual representations – even
though the task is noncontextual (since we do not have different
ground-truths for an object occurring in different contexts in our
setting). Also, despite being weaker than BERT on downstream NLP tasks,
ELMo does better on scalar probing, consistent with it being better at
numeracy due
to its character-level tokenization.
Zero-shot transfer
We note that DoQ is derived heuristically from web text and contains
noise. So we also evaluate probes trained on DoQ on 2 datasets
containing ground truth labels of scalar attributes:
VerbPhysics and
Amazon Price
Dataset.
The first is a human labeled dataset of relative comparisons, e.g.
(person, fox, weight, bigger). Predictions for this task are made by
comparing the point estimates for rgr and highest-scoring buckets for
mcc. The second is a dataset of empirical distributions of product
prices on Amazon. We retrained a probe on DoQ prices using 12 power-of-4
buckets to support finer grained predictions.
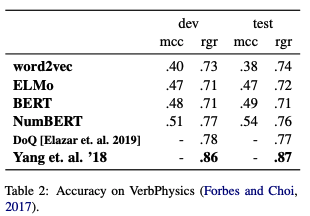
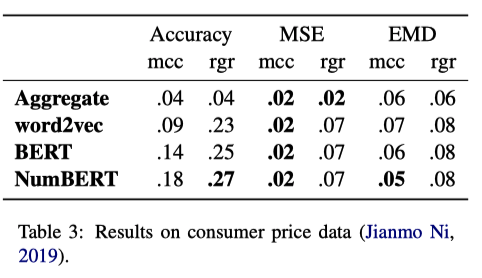
The results are shown in the tables above. On VerbPhysics (the table on
the top), rgr+NumBERT performed best, approaching the performance of
using DoQ as an oracle, though short of specialized
models for
this task. Scalar probes trained with mcc perform poorly, possibly
because a finer-grained model of predicted distribution is not useful for
the 3-class comparative task. On the Amazon Price Dataset (the table on
the bottom) which is a full distribution prediction task, mcc+NumBERT did
best on both distributional metrics. On both zero-shot transfer tasks,
NumBERT representations were the best across all configurations of
metrics/objectives, suggesting that manipulating numeric representations
of the text in the pre-training corpora can significantly improve
performance on scale prediction.
Moving Forward
In the work above, we introduce a new task called scalar probing used to
measure how much information of numeric attributes of objects
pre-trained text representations have captured and find out that while
there is a significant amount of scale information in object
representations (half to a third to the theoretical upper bound), these
models are far from achieving common sense scale understanding. We also
come up with an improved version of BERT, called NumBERT, whose
representations capture scale information significantly better than all
the previous ones.
Scalar probing opens up new exciting research directions to explore. For
example, lots of work has pre-trained large-scale vision & language
models, like
ViLBERT and
CLIP.
Probing their representations to see how much scale information has been
captured and performing systematic comparisons between them and
representations learned by language-only models can be quite
interesting.
Also, models learning text representations that predict scale better can
have a great real-world impact. Consider a web query like:
“How tall is the tallest building in the world?”
With a common sense understanding of what a reasonable range of heights
for “building” is, we can detect errors in the current web QA system when there are mistakes in
retrieval or parsing, e.g. when a wikipedia sentence about a building is
mistakenly parsed as being 19 miles high instead of meters.
Check out the paper Do Language Embeddings Capture
Scales? by
Xikun Zhang, Deepak Ramachandran, Ian Tenney, Yanai Elazar, and Dan
Roth.
