The field of large language models is shifting toward lower-precision computation. This shift necessitates a rethinking of scaling laws to account for the effects of quantization on resulting quantized model performance. In this work, we demonstrate that previous conclusions on the low-bit scaling laws can be significantly sharpened by better quantization scheme design and training improvements.
We propose ParetoQ, the first algorithm that unifies binary, ternary, and 2-to-4 bit quantization-aware training. ParetoQ demonstrates its robustness by yielding state-of-the-art (SOTA) models at all bit widths, surpassing prior works tailored for individual bit levels. We’ve released the MobileLLM low-bit model collection on Hugging Face, featuring models quantized with our ParetoQ method. The smallest model is an ultra-efficient 1-bit 125M variant, with just ~16MB equivalent storage size.
These SOTA points in the Pareto chart ensure that our scaling law comparisons are both reliable and consistent, as they derive from homogeneous settings. Our scaling laws reveal that binary quantization significantly compromises accuracy, while ternary, 2-bit, and 3-bit quantization are tied in performance, often surpassing 4-bit.
ParetoQ is based on PyTorch models, including LLaMA and MobileLLM. We utilized a popular PyTorch Library: HuggingFace Transformers for accuracy experiments. For the latency experiments, we utilize the low-bit quantization kernels on the CPU with ExecuTorch. We compared their speed with that of 4-bit quantization. Additionally, we implemented state-of-the-art 2-bit GPU kernels, which showed up to a 4.14x speedup compared to FP16 and a 1.24x speedup over the Machete 4-bit kernel on TritonBench.
ParetoQ has been integrated into torchao [pull]. This integration enables users to leverage ParetoQ by specifying “paretoq” as the quantization method within torchao’s codebase. Once set, the users can utilize torchao’s ParetoQ workflow, optimizing quantization parameters to balance accuracy and compression trade-offs and compare different quantization bit`s apple-to-apple using Pareto frontier analysis. This allows for the efficient deployment of models on edge devices without requiring manual tuning of quantization settings.
To obtain the ParetoQ-quantized models, simply navigate to the torchao/prototype/paretoq directory and execute the training script:
cd torchao/prototype/paretoq && bash 1_run_train.sh $w_bit
Here, $w_bit specifies the target weight bit-width for quantization.
ParetoQ code is available at: https://github.com/facebookresearch/ParetoQ
Paper link: https://arxiv.org/abs/2502.02631
1 A Better QAT Scheduling Strategy for Extreme Low-Bit LLMs
1.1 Training Budget Allocation
Given a fixed training budget B_train = B_FPT +B_QAT, how should the budget be optimally allocated between full-precision training (B_FPT) and quantization-aware training/fine-tuning (B_QAT) to maximize the accuracy of the quantized model?
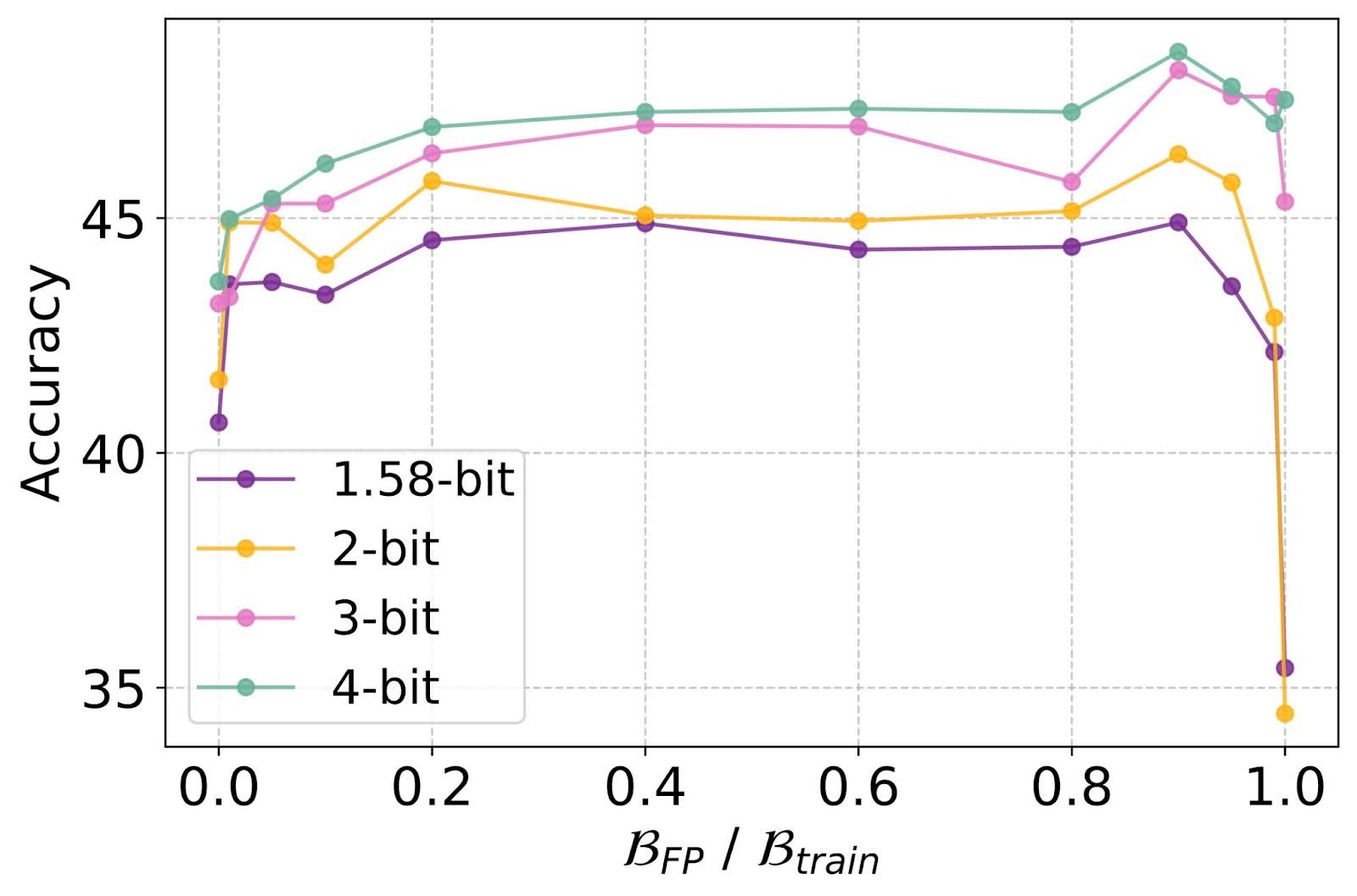
Figure 1: Optimal allocation between full-precision pretraining and QAT fine-tuning.
Finding-1 QAT finetuning consistently surpasses both PTQ with B_FPT = B_train and QAT from scratch with B_QAT = B_train. Optimal performance is nearly achieved by dedicating the majority of the training budget to full precision (FP) training and approximately 10% to QAT.
1.2 Fine-tuning Characteristics
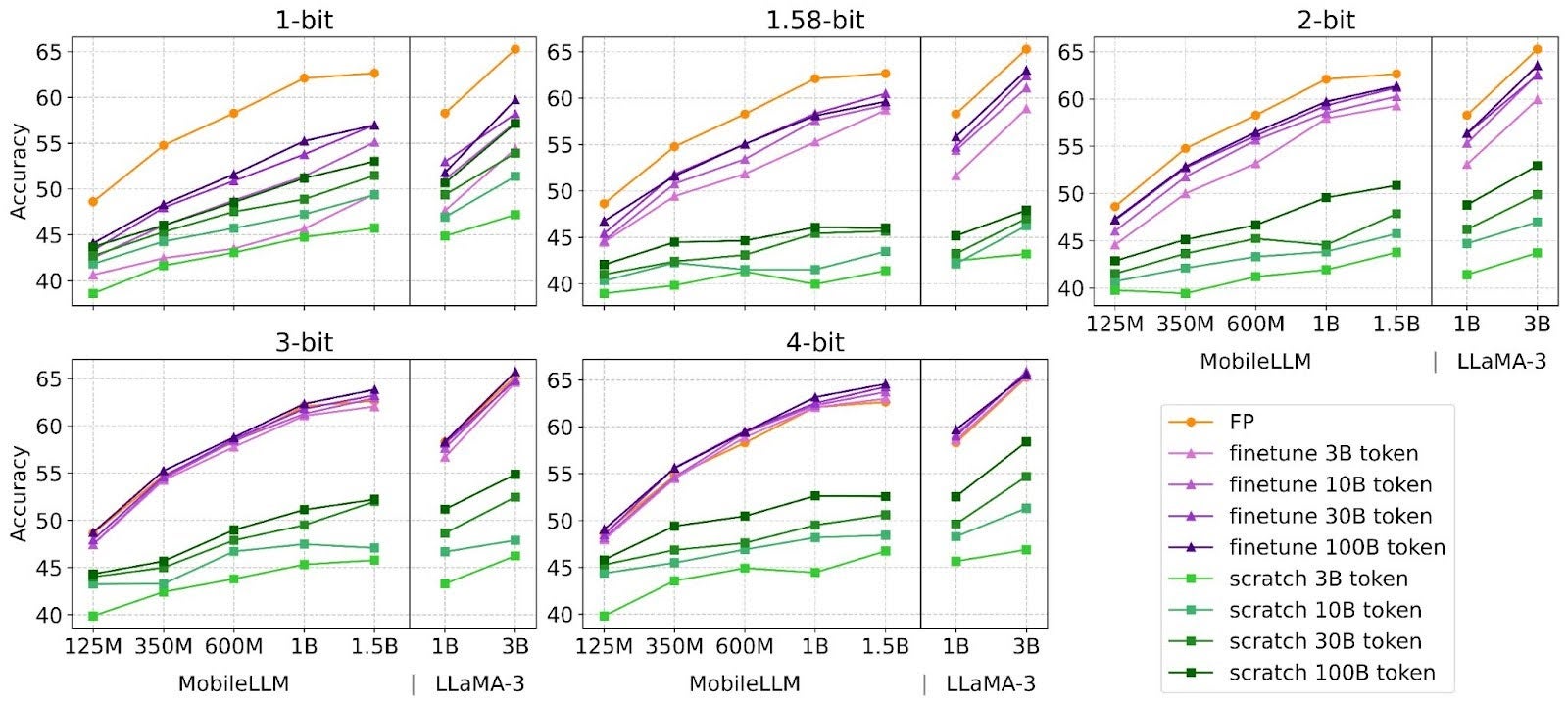
Figure 2: Analysis of training token requirements for quantization-aware fine-tuning and training from scratch
Finding-2 While fine-tuning enhances performance across all bit-widths, even binary and ternary, optimal fine-tuning effort inversely correlates with bit-width. For 3-bit and 4-bit weights, fine-tuning adjusts within a nearby grid to mitigate accuracy loss and requires less fine-tuning tokens. In contrast, binary and ternary weights break the grid, creating new semantic representations to maintain performance, requiring longer fine-tuning.
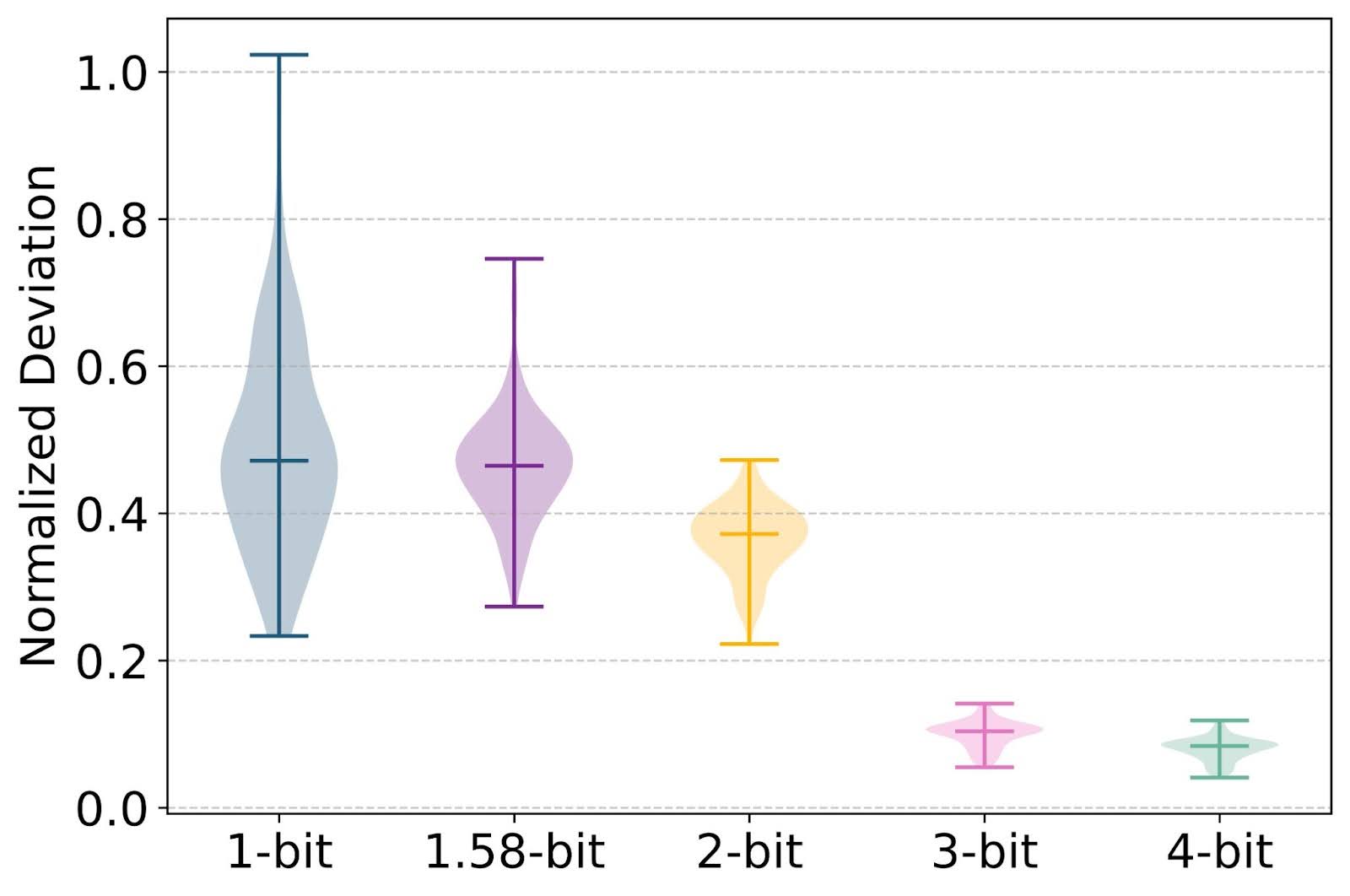
Figure 3: L1 norm difference between QAT-finetuned weights and full-precision initialization (||W_finetune −W_init||_l1 /||W_init||_l1).
2 A Hitchhiker’s Guide to Quantization Method Choices
In sub-4-bit quantization, the choice of function is highly sensitive and can drastically alter scaling law outcomes.
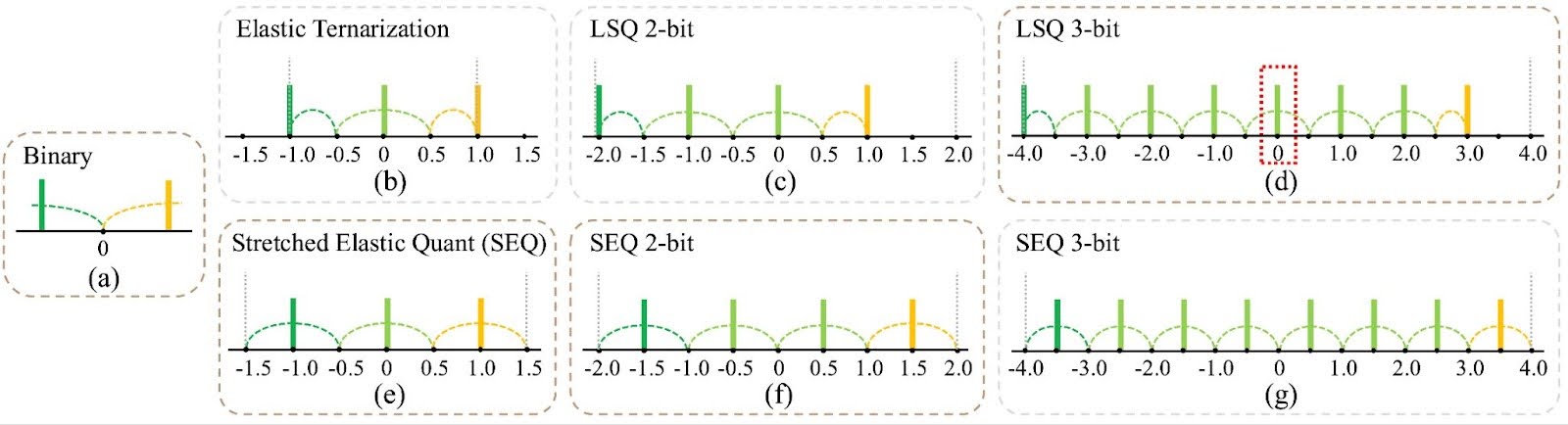
Figure 4: Impact of quantization grid choice across bit widths. 2.1.1 Range clippingCompared to statistics-based quantization (e.g., min-max quantization), learnable scales which optimize quantization ranges as network parameters, balancing outlier suppression and precision, yields more stable and superior performance. As shown in Figure (b)-(e), learnable policies consistently outperform stats-based methods across all bit widths.
2.1.2 Quantization grids
Level symmetry in quantization grids is vital for lower-bit quantization but often overlooked. Including “0” in even-level quantization (e.g., 2-bit, 3-bit, 4-bit) can cause imbalance. For instance, 2-bit quantization options like (-2, -1, 0, 1) limit positive representation to only one level, while (-1.5, -0.5, 0.5, 1.5) offers more balanced representation. We propose Stretched Elastic Quant (SEQ) to address this in lower-bit scenarios.
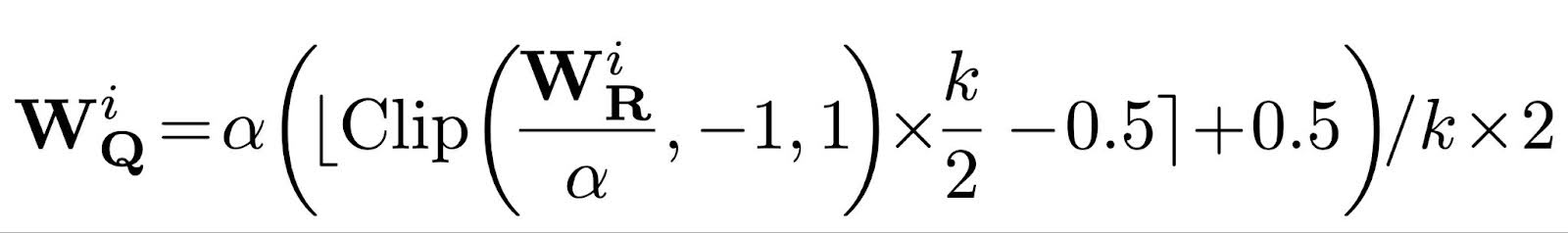
SEQ balances quantized levels and evenly divides the full-precision weight span, crucial for extremely low-bit quantization. Figures show SEQ’s advantage in ternary and 2-bit quantization, while LSQ with “0” slightly excels in 3 and 4-bit cases.
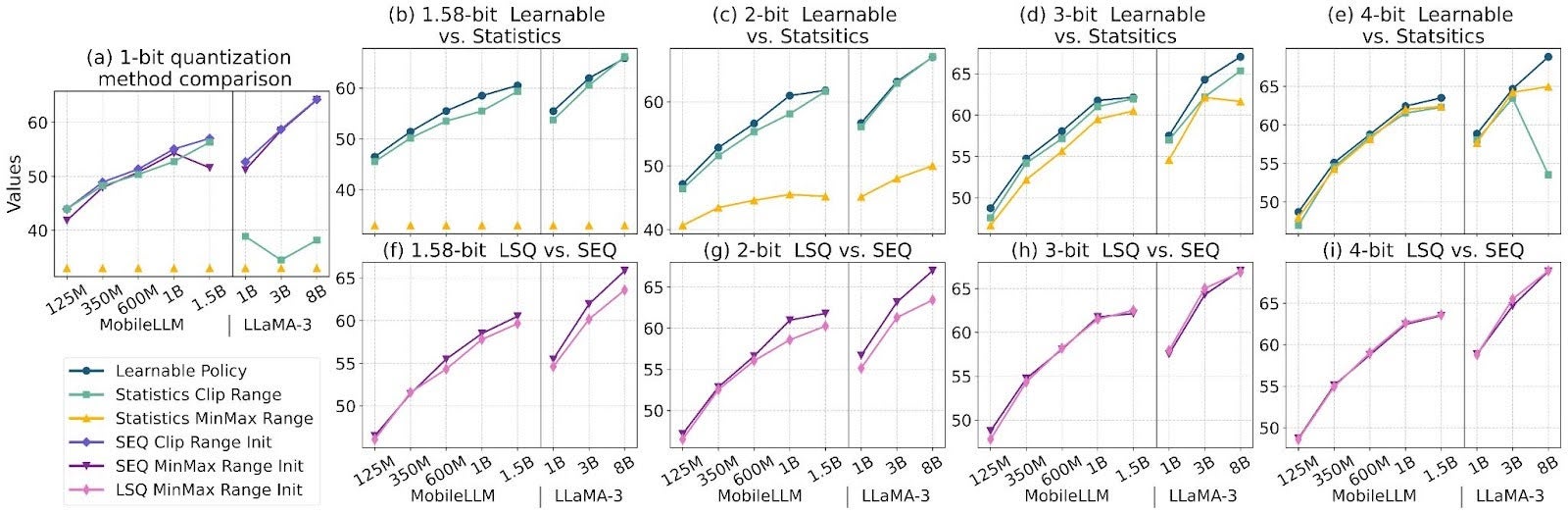
Figure 5: Comparison of quantization methods across different bit-widths
2.2 Quantization Function
Based on our analysis, we combine the optimal quantization functions identified for each bit-width into one formula, denoted as ParetoQ. This includes Elastic Binarization [1] for 1-bit quantization, LSQ [2] for 3 and 4-bit quantization, and the proposed SEQ for 1.58 and 2-bit quantization.
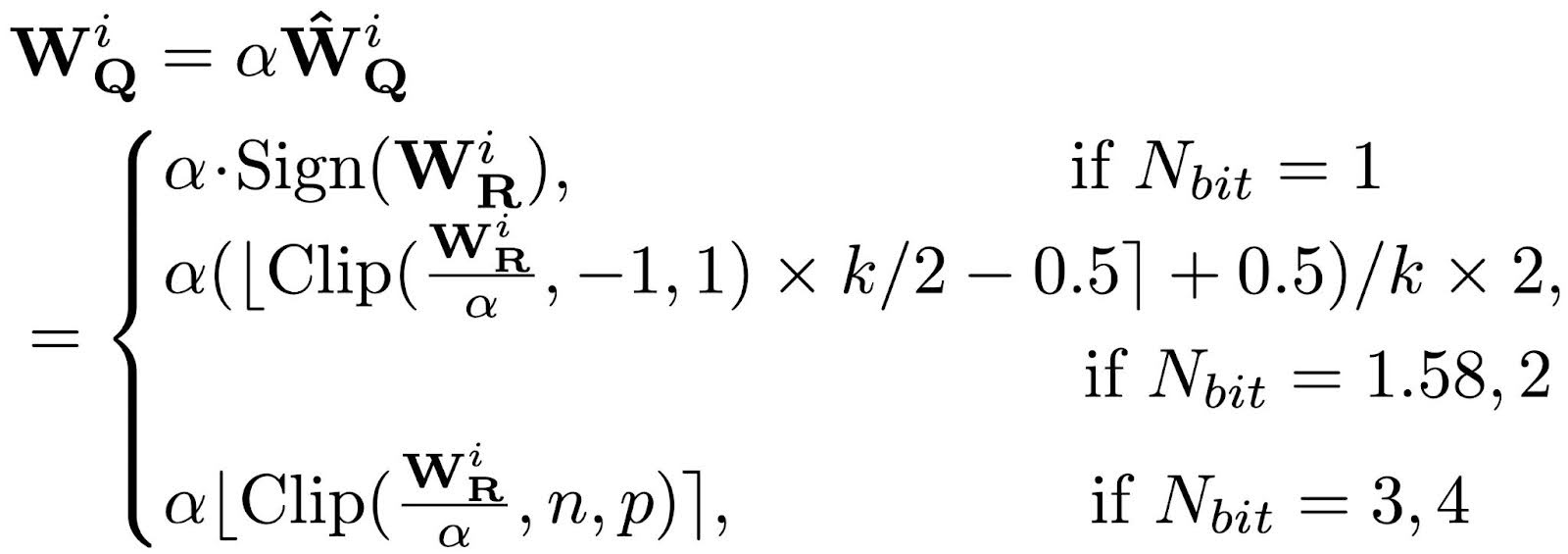
Here, k equals 3 in the ternary case and 2Nbit otherwise; n = –2Nbit-1 and p = 2Nbit-1 -1. In the backward pass, the gradients to the weights and scaling factor can be easily calculated using a straight-through estimator.
With ParetoQ, we present a robust comparison framework across five bit-widths (1-bit, 1.58-bit, 2-bit, 3-bit, 4-bit), each achieving state-of-the-art accuracy. This facilitates direct, apple-to-apple comparisons to identify the most effective bit-width selection.
3 Comparison with SoTA
3.1 Comparisons on 1.58-bit quantization
The figure below illustrates that ParetoQ consistently outperforms previous methods targeting ternary quantization aware training including Spectra [3] and 1-bit Era [4]. Given that a full-precision LLaMA-3 3B model achieves 69.9 accuracy, it’s remarkable that ParetoQ ternary 3B-parameter model narrows the gap to just 4.1 points, while previous methods experience drops exceeding 11.7 points.
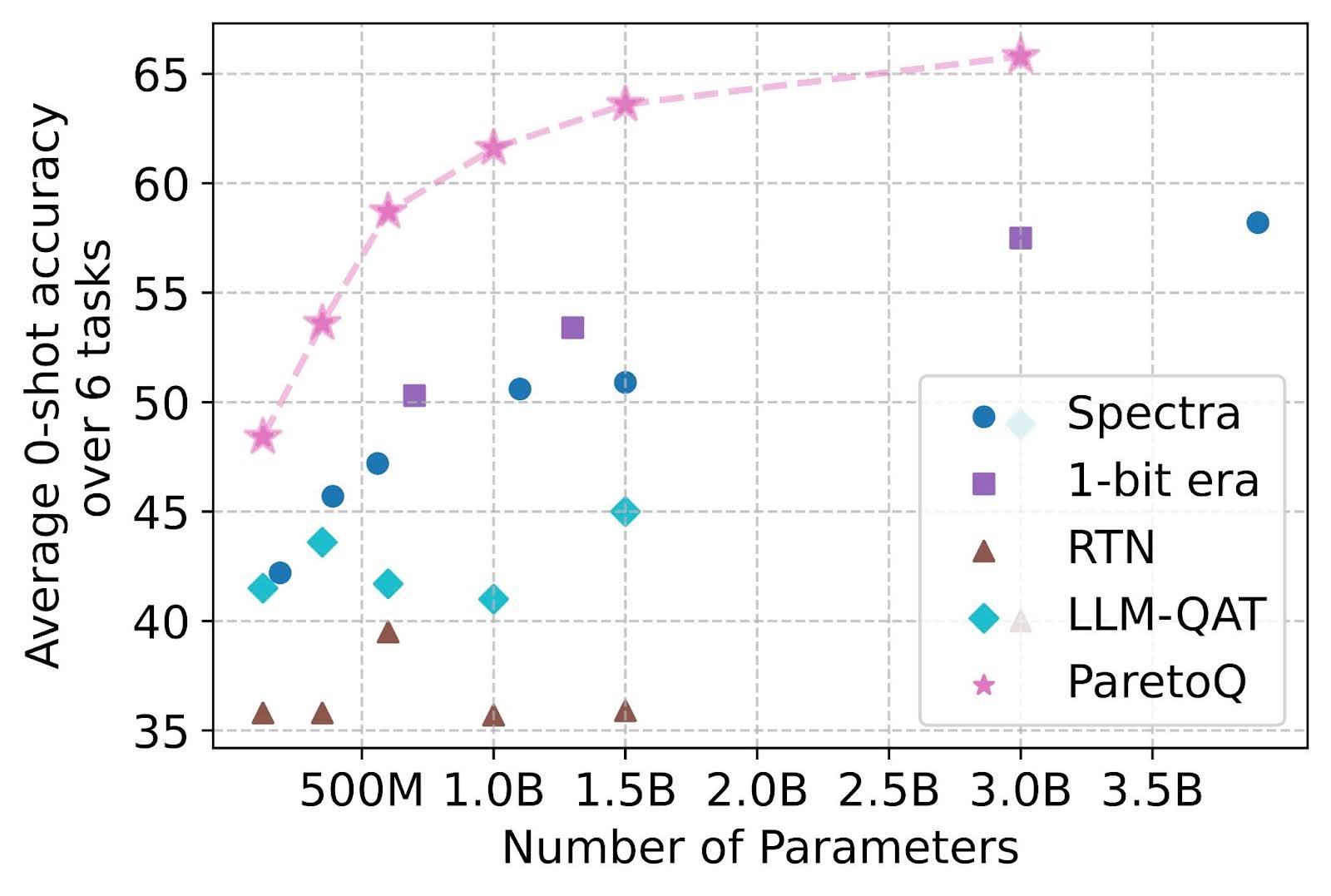
Figure 6: Ternary quantization accuracy averaged across six tasks: ARC-e, ARC-c, BoolQ, PIQA, HellaSwag, and WinoGrande. ParetoQ consistently outperforms all prior methods in ternary quantization-aware training.
3.2 comparisons 2-bit / 3-bit / 4-bit quantization
As evidenced by Figure 1, compared to previous state-of-the-art PTQ and QAT methods on 2, 3 or 4-bit quantization settings, our approach consistently resides on the Pareto front, with a particularly pronounced advantage in lower-bit quantization settings. These results confirm that our bit-accuracy trade-off conclusions are benchmarked against SoTA results across all bit settings, ensuring its reliability.
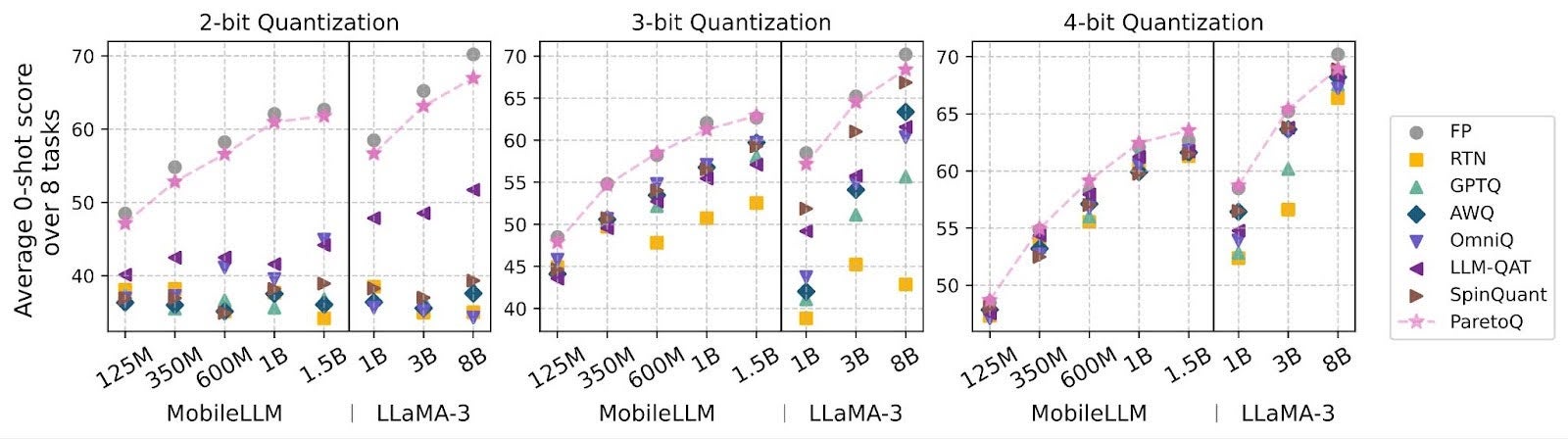
Figure 7: Accuracy comparison on 8 models. ParetoQ outperforms all state-of-the-art PTQ and QAT methods in 2, 3, and 4-bit settings.
4 Pareto Curve
4-bit quantization-aware training (QAT) achieves near-lossless compression in many scenarios. With ParetoQ, we are able to further improve the trade-off curve. Figure (a) demonstrates that sub-4-bit quantization, including binary, ternary, 2-bit, and 3-bit, often surpasses 4-bit. Notably, 2-bit and ternary models reside on the Pareto frontier.
To evaluate potential speedup benefits beyond memory reduction, we utilize the High-Performance Low-Bit Operators for 2-bit quantization and compare the latency with 4-bit quantization. The curves in Figure8 (c) demonstrate that, within our experimental range, 2-bit quantized models consistently outperform 4-bit models in terms of accuracy-speed performance, positioning 2-bit quantization as a superior choice for on-device applications where both latency and storage are critical.
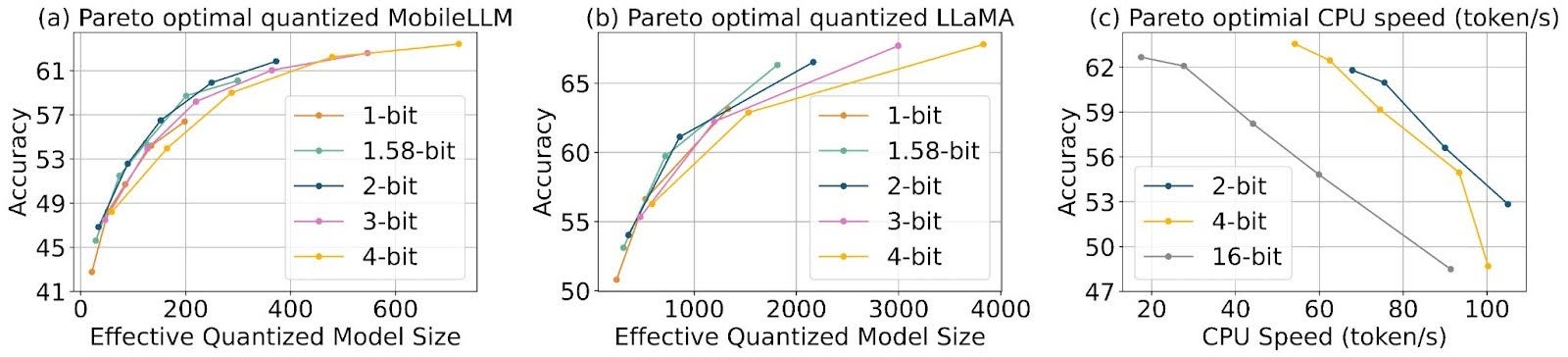
Figure 8: (a) (b) In sub-4-bit regime, 1.58-bit, 2-bit, and 3-bit quantization outperform 4-bit in terms of the accuracy-model size trade-off. (c) Under hardware constraints, 2-bit quantization demonstrates superior accuracy-speed trade-offs compared to higher-bit schemes.
5 GPU Latency
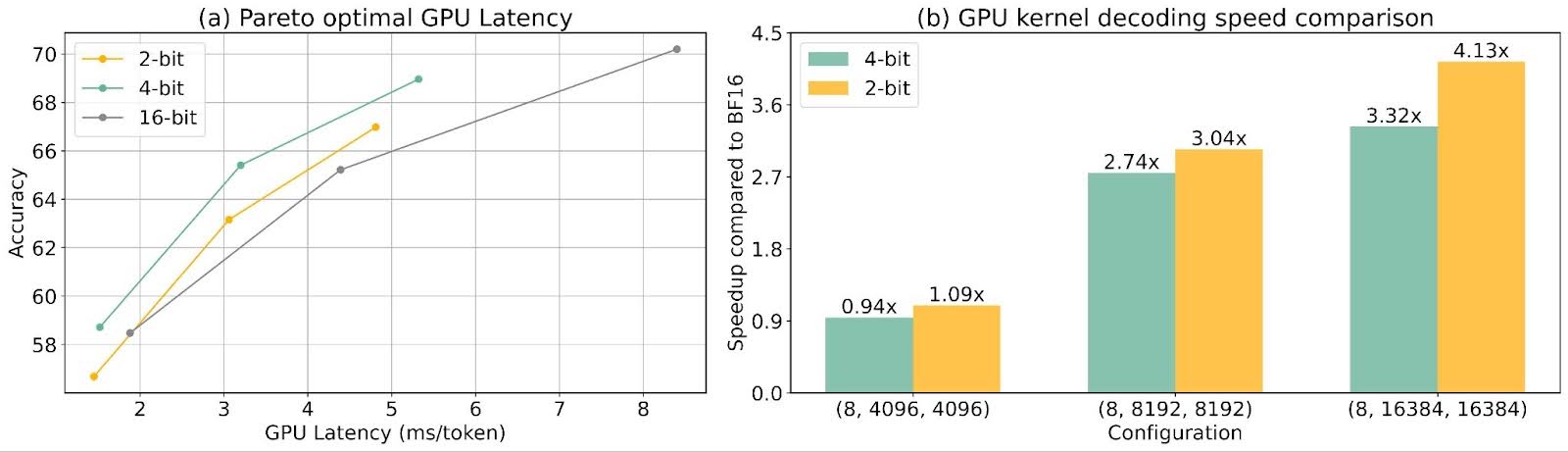
We measured the latency of LLaMA 3.2 models (1B, 3B, 8B) on an H100 NVL GPU (94GB memory). The W4A16 kernel used the Machete kernel from vLLM, while the W2A16 kernel was implemented based on the CUTLASS mixed precision backbone kernel. All tests were performed on a single GPU with a context length of 2048 tokens. For kernel-level latency, we compared the 2-bit kernel to the 4-bit Machete kernel across three weight shapes: (4096 x 4096), (8192 x 8192), and (16384 x 16384) on TritonBench. For larger size kernels, 2-bit can achieve ~24% speed up compared to the 4-bit Machete kernel.
Conclusion
In this study, we propose ParetoQ, an advanced quantization framework that achieves state-of-the-art performance across all bit-width levels. This framework uniquely enables a direct, consistent comparison across different bit-widths, ensuring an equitable evaluation of performance metrics. Our empirical analysis indicates that quantization at 1.58-bit, 2-bit, and 3-bit offers a superior trade-off between accuracy and effective quantized model size compared to 4-bit, highlighting their potential for optimized model deployment.
Feel free to try running ParetoQ from torchao/prototype/paretoq, following the steps in that repo. If you have any questions, feel free to reach out to Zechun Liu <zechunliu@meta.com>, Changsheng Zhao <cszhao@meta.com> Andrew Or <andrewor@meta.com>
References
[1] BiT: Robustly Binarized Multi-Distilled Transformer.
[2] Learned Step Size Quantization.
[3] Spectra: A Comprehensive Study of Ternary, Quantized, and FP16 Language Models.
[4] The Era of 1-bit LLMs: All Large Language Models Are in 1.58 Bits
