Safety Validation of Black-Box Autonomous Systems

With autonomous systems becoming more capable, they are entering into safety-critical domains such as autonomous driving, aircraft collision avoidance, and healthcare. Ensuring the safe operations of these systems is a crucial step before they can be deployed and accepted by our society. Failure to perform the proper degree of safety validation can risk the loss of property or even human life.

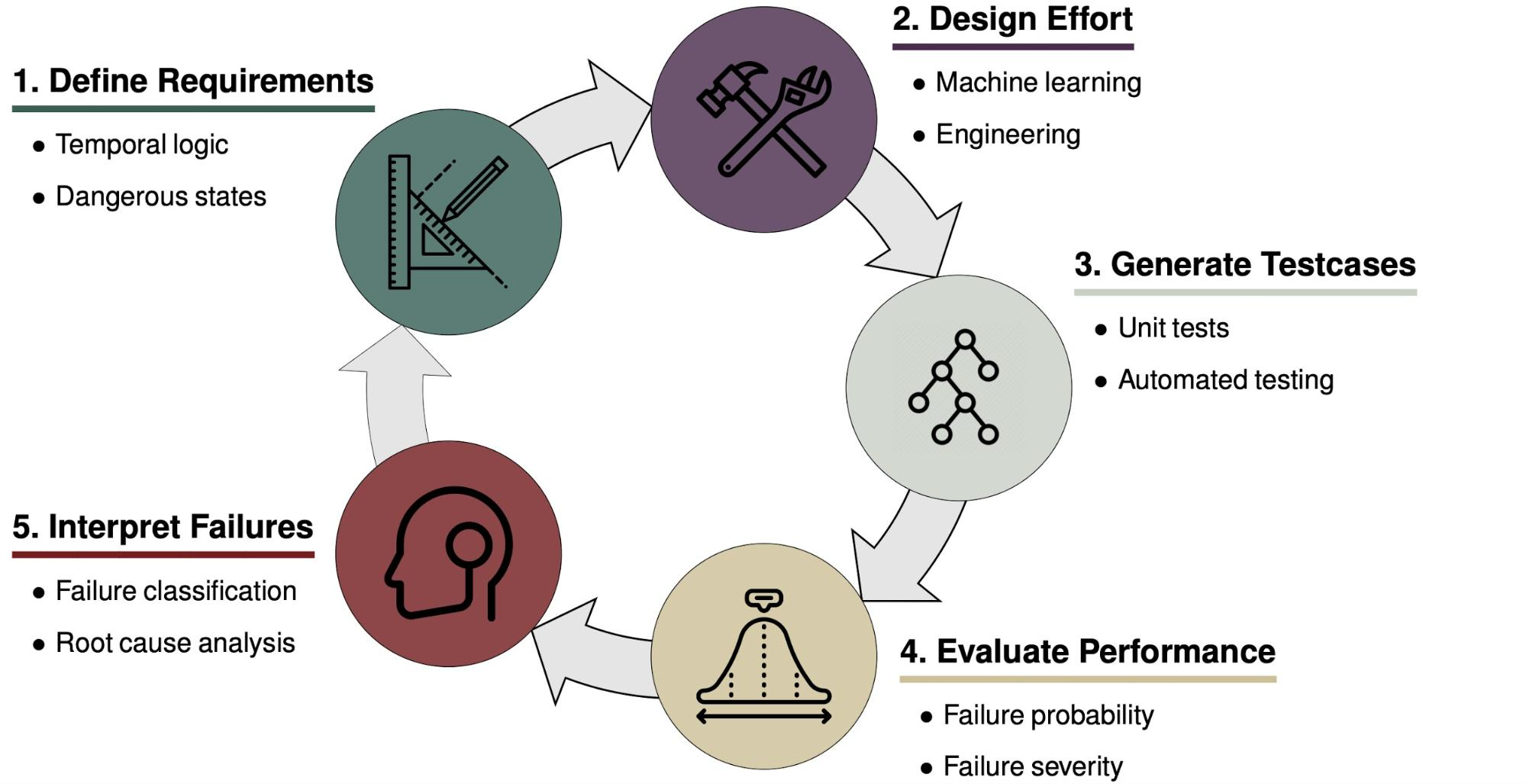
Safety can be incorporated at various stages of the development of an autonomous system. Consider the above model for the design cycle of such a system. A necessary component of safety is the definition of a complete set of realistic and safe requirements such as the Responsibility-Sensitive Safety model¹ which encodes commonsense driving rules—such as don’t rear end anyone and right of way is given, not taken—into formal mathematical statements about what a vehicle is and is not allowed to do in a given driving scenario. Safety can also be incorporated directly into the design of the system through techniques such as safety-masked reinforcement learning (RL)² where a driving agent learns how to drive under the constraint that it only takes actions that have a minimal likelihood of causing a collision. Compared to traditional reinforcement learning techniques which have no constraint on their exploratory actions, safety-masked RL results in a safer driving policy.

Once a prototype of a system is available, safety validation can be performed through testing, performance evaluation, and interpretation of the failure modes of the system. Testing can discover failures due to implementation bugs, missing requirements, and emergent behavior due to the complex interaction of subcomponents. For complex autonomous systems operating in physical environments, we can not guarantee safety in all situations, so performance evaluation techniques can determine if the system is acceptably safe. The failure examples generated from testing can then be used to understand flaws in the systems and help engineers to fix them in the next iteration. Even with safety embedded in the process of defining requirements and system design, safety validation is a critical part of ensuring safe autonomy.

There are multiple ways to go about safety validation. White-box approaches use knowledge of the design of the system to construct challenging scenarios and evaluate the behavior of the system. They are often interpretable and can give a high degree of confidence in a system, but can suffer from problems of scalability. Modern autonomous systems employ complex components such as deep neural networks for perception and decision making. Despite improvements to white-box approaches for small neural networks³, they don’t scale to the large networks used in practice. We can, however, trade formal guarantees for scalability by employing algorithms that treat the autonomous system as a black-box.

Safety validation algorithms for black-box autonomous systems have become the preferred tool for validation since they scale to complex systems and can rely on the latest advancements in machine learning to become more effective. In this blog post we cover the latest research in algorithms for the safety validation of black box autonomous systems. For a more in-depth description of the following algorithms (including pseudocode) see our recent survey paper A Survey of Algorithms for Black-Box Safety Validation.

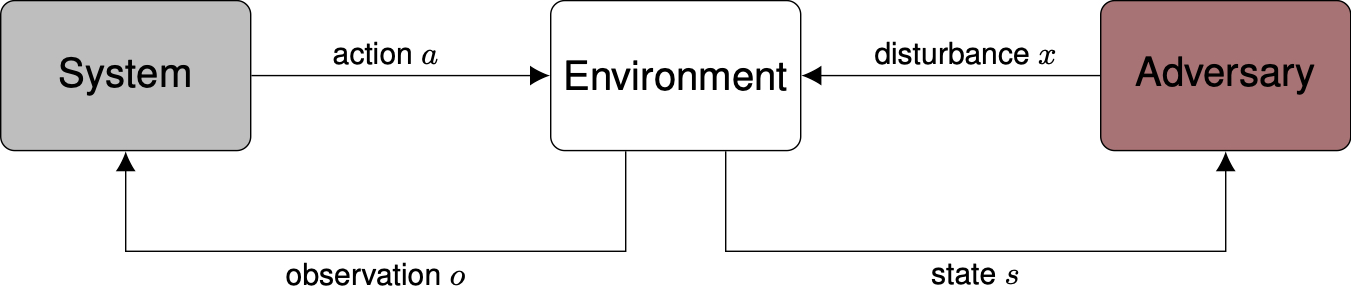
The setup for safety validation algorithms for black-box systems is shown above. We have a black-box system that is going to be tested, such as an autonomous vehicle driving policy or an aircraft collision avoidance system. We assume we have a simulated environment in which the system takes actions after making observations with its sensors, while an adversary perturbs the environment through disturbances in an effort to make the system fail. Disturbances could include sensor noise, the behavior of other agents in the environment, or environmental conditions such as weather. The adversary may have access to the state of the environment which, for example, may describe the positions and velocity of all the vehicles and pedestrians in a driving scenario. The systems we care about usually operate over time in a physical environment, in which case the adversary seeks to find the sequence of disturbances that leads to failure. Finding a disturbance trajectory that leads to failure, rather than just a single disturbance, makes the problem much more challenging. We may also have a model of the disturbances in the environment that describes which sequences of disturbances are most likely. The disturbance model can be constructed through expert knowledge or learned from real-world data. The exact goal of the adversary may be

1. Falsification: Find any disturbance trajectory that leads to a failure.
2. Most likely failure analysis: Find the most likely disturbance trajectory that leads to a failure (i.e. maximize ).
3. Estimation of the probability of failure: Determine how likely it is that any failure will occur based on knowledge of .

The adversary can use a variety of algorithms to generate disturbances. We will cover 4 categories: optimization, path-planning, reinforcement learning, and importance sampling.

Optimization

Optimization approaches search over the space of possible disturbance trajectories to find those that lead to a system failure. Optimization techniques can involve adaptive sampling or a coordinated search, both of which are guided by a cost function which measures the level of safety for a particular disturbance trajectory. The lower the cost, the closer we are to a failure. Some common cost functions include

• Miss distance: Often a physically-motivated measure of safety such as the point of closest approach between two aircraft or two vehicles.
• Temporal logic robustness: When the safety requirements of a system are expressed formally using temporal logic, a language used to reason about events over time, the robustness⁴ measures how close a trajectory is to violating the specification⁵.

When performing most likely failure analysis, the probability of the disturbance trajectory is incorporated into the regular cost function to produce a new cost . Ideally, probability can be incorporated as a piecewise objective where when does not lead to failure and when does lead to a failure. In practice, however, using a penalty term may be easier to optimize.

The upside of formulating safety validation as an optimization problem is the ability to use off-the-shelf optimizers and rely on the significant amount of optimization literature (see Kochenderfer and Wheeler⁶ for an overview). Approaches that have been successfully used for safety validation include simulated annealing⁷, genetic algorithms⁸, Bayesian optimization⁹, extended ant-colony optimization¹⁰, and genetic programming¹¹.

The downsides of optimization-based approaches are twofold. First, we are directly searching over the space of all possible disturbance trajectories which is exponential in the length of the trajectory. This can quickly get out of hand. Second, the state of the environment is not typically used when choosing the disturbance trajectory. The state of the environment may not be available for logistical or privacy reasons, but if it is, then the state can provide additional information to the adversary. The next two sections describe techniques to address these limitations by building the disturbance trajectories sequentially and using the state information to help guide the search.

Path Planning

When the safety validation problem is cast as a path-planning problem, we search for failures by sequentially building disturbance trajectories that explore the state space of the environment. There are several metrics of state-space coverage that can be used to guide the search and decide when the state space has been sufficiently explored¹².

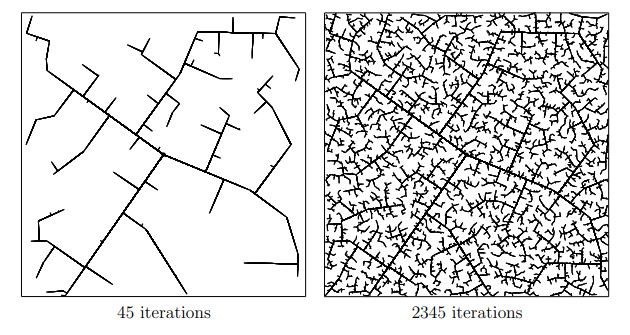
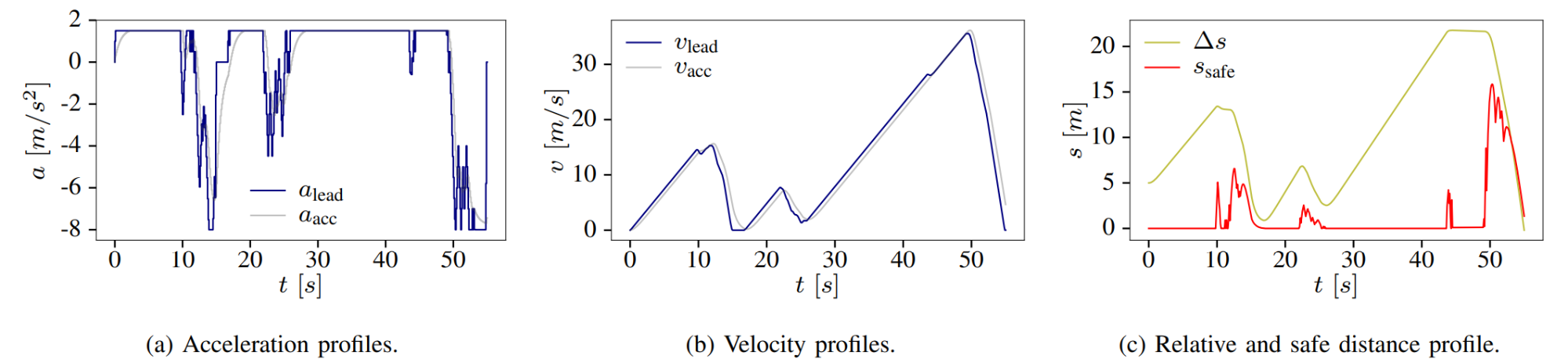
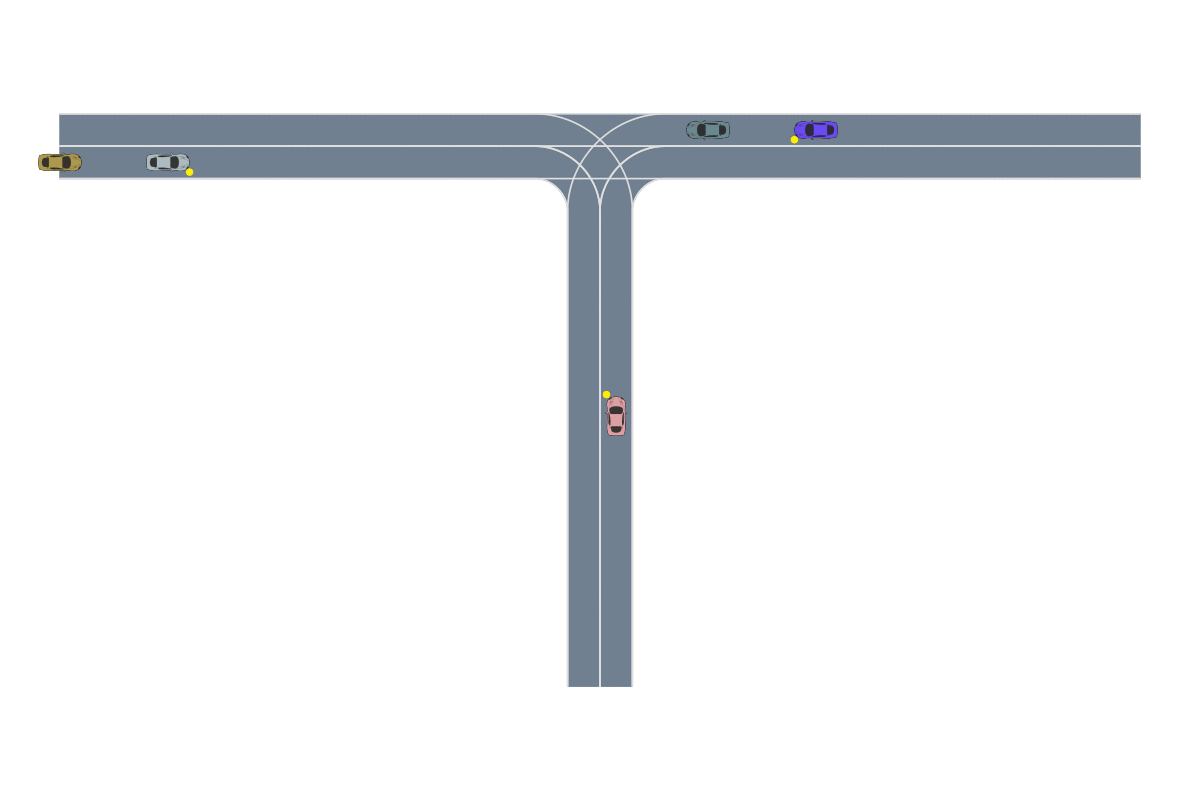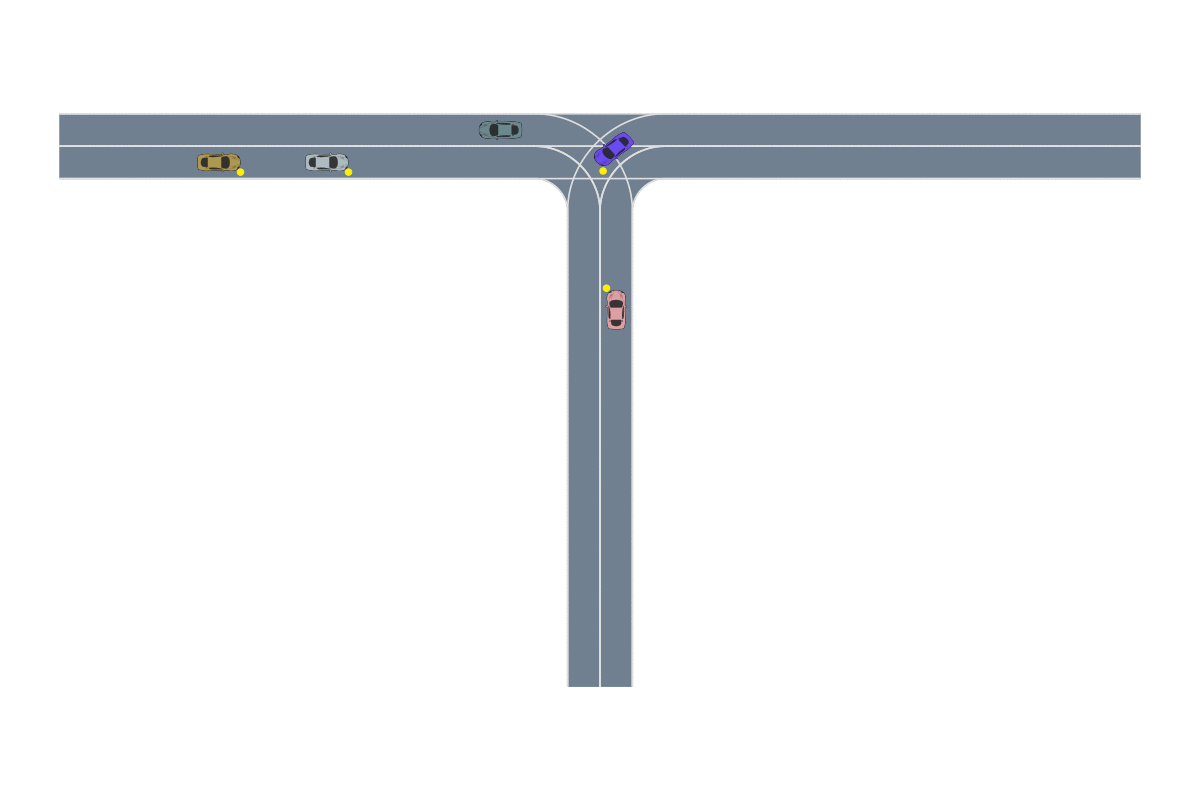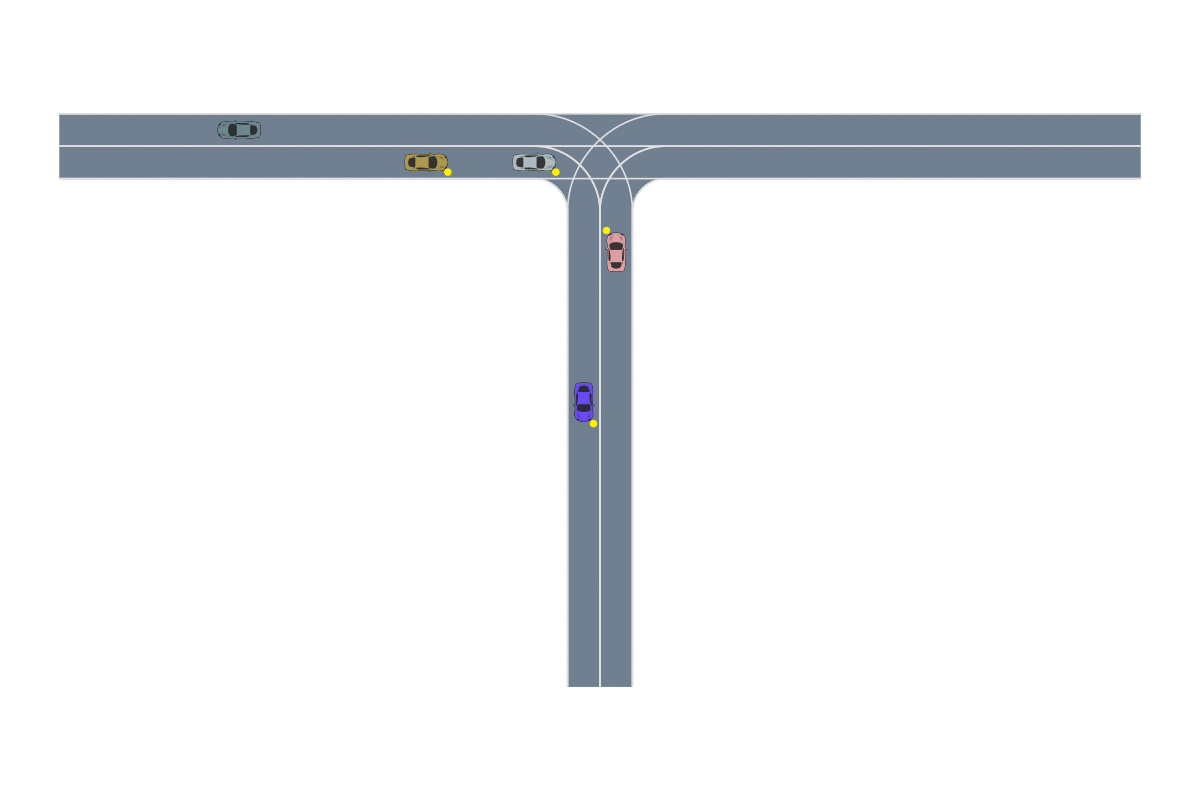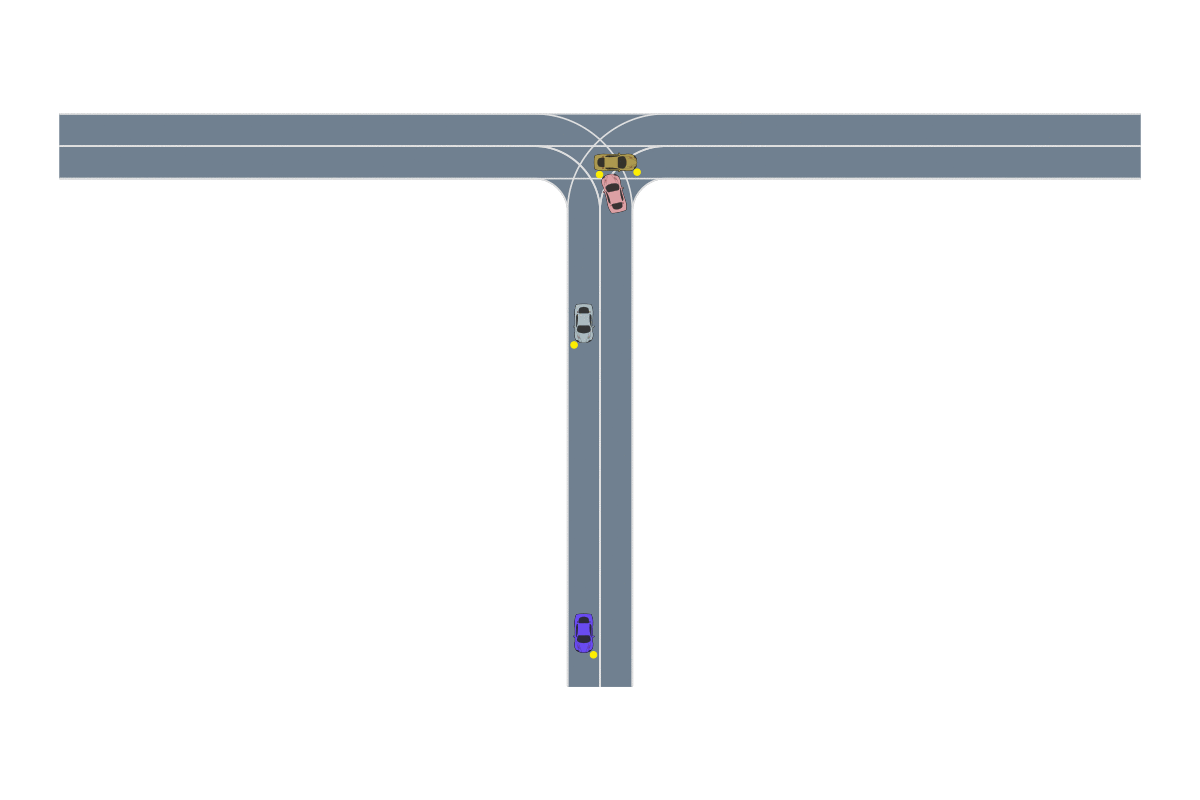
One of the most common path-planning algorithms that has been used for safety validation is the rapidly-exploring random tree (RRT) algorithm, depicted above¹³. In RRT, a space-filling tree is iteratively constructed by choosing disturbances that bring the environment into unexplored regions of the state space. The RRT algorithm has been used to find failures of an adaptive cruise control system¹⁴ where failures involved complex motion of the lead vehicle (shown below) that would be rarely discovered by traditional sampling techniques.

Many path planning approaches were designed to be used with white-box systems and environments where dynamics and gradient information is available. When applied to black-box safety validation, these algorithms need to be adapted to forego the use of such information. For example, in multiple shooting methods, a trajectory is constructed through disjoint segments, which are then joined using gradient descent. In the absence of gradient information, a black-box multiple shooting method was developed that connected segments by successively refining the segment inputs and outputs through full trajectory rollouts¹⁵.

Reinforcement Learning

The safety validation problem can be further simplified if we describe it as a Markov decision process where the next state of the environment is only a function of the current state and disturbance. The Markov assumption allows us to select disturbances based only on the current state and apply reinforcement learning (RL) algorithms such as Monte Carlo tree search (MCTS), and deep RL algorithms such as Deep Q-Networks or Proximal Policy Optimization.

Monte Carlo tree search is similar to RRT in that a search tree is iteratively created to find disturbance trajectories that end in failure. Unlike RRT, however, MCTS is designed for use with black-box systems. The trajectories are always rolled out from the initial state of the simulator and the search is guided by a reward function rather than a coverage of the state space. These modifications allow MCTS to be applied in the most information-poor environments. Lee et. al¹⁶ used MCTS to find failures of an aircraft collision avoidance system (an example failure is depicted below) where they had no access to the simulator state and could only control actions through a pseudorandom seed. This approach may be preferred when organizations don’t want to expose any aspect of the functioning of their system.

Deep RL has seen a lot of success in recent years due to its ability to solve problems with large state spaces, complex dynamics, and large action spaces. The success of deep RL is due to the large representational capacity of neural networks and advanced optimization techniques, which make it a natural choice as a safety validation algorithm. For example, it has been used to find failures of autonomous driving policies¹⁷ where the state and action spaces are large and continuous—attributes that are difficult for other algorithms to handle well. A sample failure of an autonomous driving policy is demonstrated below¹⁸.

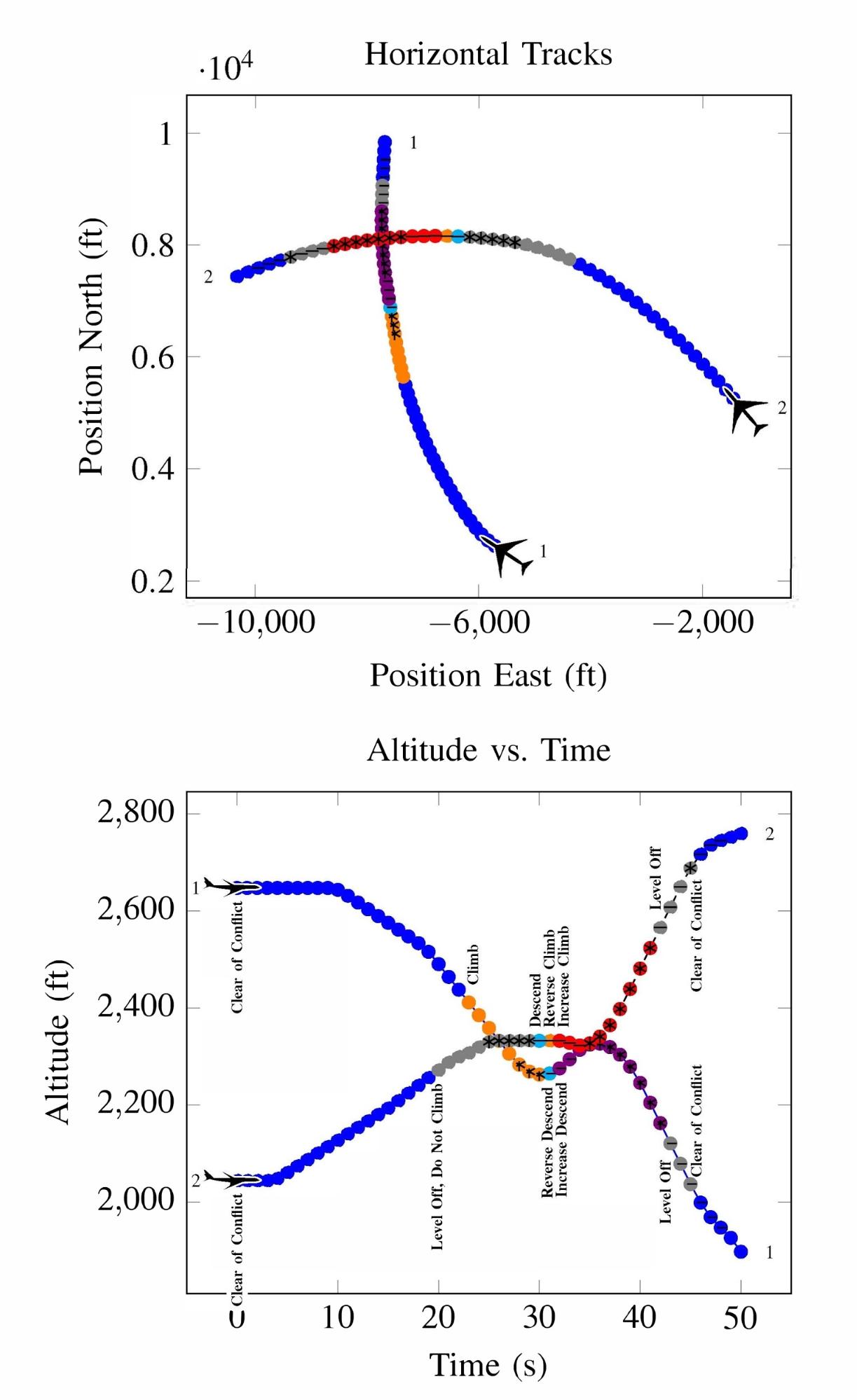
Optimization, path-planning and RL approaches all lend themselves to solving the problems of falsification and most likely failure analysis. However, when we need to evaluate the failure probability of a system, importance sampling approaches should be used.

Importance Sampling

The final set of approaches are well-suited for the task of estimating the probability of failure of the system from many failure examples. Importance sampling approaches seek to learn a sampling distribution that reliably produces failures and can be used to estimate the probability of failure with the minimal number of samples. Some common approaches are the cross-entropy method¹⁹, multilevel splitting²⁰, supervised learning²¹, and approximate dynamic programming²².

Most importance sampling approaches suffer the same drawback as optimization-based approaches: they are constructing a distribution across the entire disturbance trajectory . If we can invoke the Markov assumption, however, then we can construct a good sampling distribution based only on the current state using dynamic programming. However, the downside to dynamic programming is its inability to scale to large state spaces and thus complex scenarios. Our recent work²³ shows that we can overcome this scalability problem by decomposing the system into subproblems and combining the subproblem solutions. For example, in an autonomous driving scenario, each adversarial agent on the road is paired with the ego vehicle to create a smaller safety validation problem with just two agents. Each of these problems are solved and then recombined using a neural network based on the Attend, Adapt and Transfer (A2T) architecture²⁴. The combined solution is then refined using simulations of the full scenario. The decomposition strategy, network architecture and a sample failure for a 5-agent driving scenario is shown below. These types of hybrid approaches will be required to solve the most challenging safety validation problems.

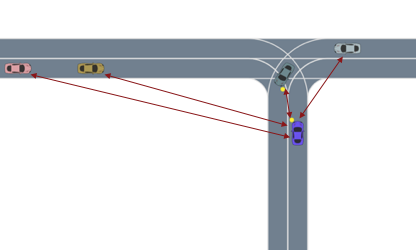
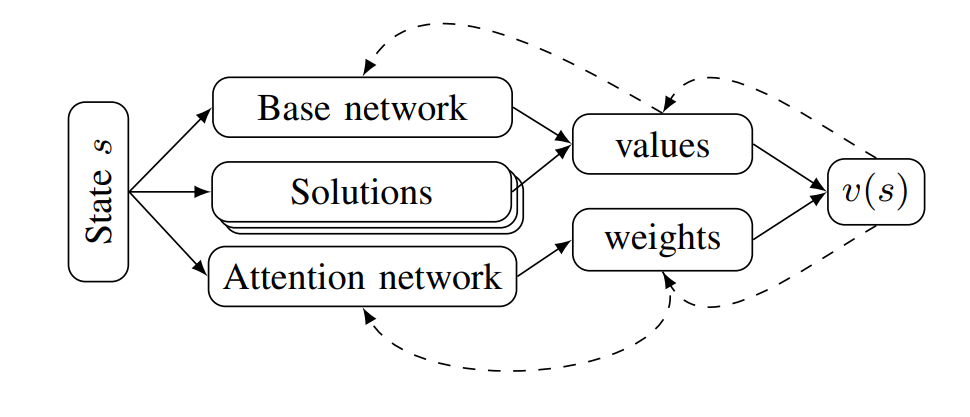
The Future

The validation of complex and safety-critical autonomous systems will likely involve many different techniques throughout the system design cycle, and black-box safety validation algorithms will play a crucial role. In particular, black-box algorithms are useful to the engineers who design safety-critical systems as well as third-party organizations that wish to validate the safety of such systems for regulatory or risk-assessment purposes. Although this post reviews many algorithms that will be of practical use for the validation of safety-critical autonomous systems, there are still areas that require more investigation. For example, we would like to be able to answer the question: if no failure has been found, how sure are we that the system is safe? This will require the development of algorithms that have formal or probabilistic guarantees of convergence. Scalability also remains a significant challenge. Autonomous systems can encounter a wide range of complex interactions, so safety validation algorithms must be able to efficiently discover failures in the most complex scenarios. The algorithms presented in this survey are a promising step toward safe and beneficial autonomy.

Acknowledgements

Many thanks to Michelle Lee, Andrey Kurenkov, Robert Moss, Mark Koren, Ritchie Lee, and Mykel Kochenderfer for comments and edits on this blog post.

Read More