For a machine learning (ML) algorithm to be effective, useful features must be extracted from (often) large amounts of training data. However, this process can be made challenging due to the costs associated with training on such large datasets, both in terms of compute requirements and wall clock time. The idea of distillation plays an important role in these situations by reducing the resources required for the model to be effective. The most widely known form of distillation is model distillation (a.k.a. knowledge distillation), where the predictions of large, complex teacher models are distilled into smaller models.
An alternative option to this model-space approach is dataset distillation [1, 2], in which a large dataset is distilled into a synthetic, smaller dataset. Training a model with such a distilled dataset can reduce the required memory and compute. For example, instead of using all 50,000 images and labels of the CIFAR-10 dataset, one could use a distilled dataset consisting of only 10 synthesized data points (1 image per class) to train an ML model that can still achieve good performance on the unseen test set.
 |
| Top: Natural (i.e., unmodified) CIFAR-10 images. Bottom: Distilled dataset (1 image per class) on CIFAR-10 classification task. Using only these 10 synthetic images as training data, a model can achieve test set accuracy of ~51%. |
In “Dataset Meta-Learning from Kernel Ridge Regression”, published in ICLR 2021, and “Dataset Distillation with Infinitely Wide Convolutional Networks”, presented at NeurIPS 2021, we introduce two novel dataset distillation algorithms, Kernel Inducing Points (KIP) and Label Solve (LS), which optimize datasets using the loss function arising from kernel regression (a classical machine learning algorithm that fits a linear model to features defined through a kernel). Applying the KIP and LS algorithms, we obtain very efficient distilled datasets for image classification, reducing the datasets to 1, 10, or 50 data points per class while still obtaining state-of-the-art results on a number of benchmark image classification datasets. Additionally, we are also excited to release our distilled datasets to benefit the wider research community.
Methodology
One of the key theoretical insights of deep neural networks (DNN) in recent years has been that increasing the width of DNNs results in more regular behavior that makes them easier to understand. As the width is taken to infinity, DNNs trained by gradient descent converge to the familiar and simpler class of models arising from kernel regression with respect to the neural tangent kernel (NTK), a kernel that measures input similarity by computing dot products of gradients of the neural network. Thanks to the Neural Tangents library, neural kernels for various DNN architectures can be computed in a scalable manner.
We utilized the above infinite-width limit theory of neural networks to tackle dataset distillation. Dataset distillation can be formulated as a two-stage optimization process: an “inner loop” that trains a model on learned data, and an “outer loop” that optimizes the learned data for performance on natural (i.e., unmodified) data. The infinite-width limit replaces the inner loop of training a finite-width neural network with a simple kernel regression. With the addition of a regularizing term, the kernel regression becomes a kernel ridge-regression (KRR) problem. This is a highly valuable outcome because the kernel ridge regressor (i.e., the predictor from the algorithm) has an explicit formula in terms of its training data (unlike a neural network predictor), which means that one can easily optimize the KRR loss function during the outer loop.
The original data labels can be represented by one-hot vectors, i.e., the true label is given a value of 1 and all other labels are given values of 0. Thus, an image of a cat would have the label “cat” assigned a 1 value, while the labels for “dog” and “horse” would be 0. The labels we use involve a subsequent mean-centering step, where we subtract the reciprocal of the number of classes from each component (so 0.1 for 10-way classification) so that the expected value of each label component across the dataset is normalized to zero.
While the labels for natural images appear in this standard form, the labels for our learned distilled datasets are free to be optimized for performance. Having obtained the kernel ridge regressor from the inner loop, the KRR loss function in the outer loop computes the mean-square error between the original labels of natural images and the labels predicted by the kernel ridge regressor. KIP optimizes the support data (images and possibly labels) by minimizing the KRR loss function through gradient-based methods. The Label Solve algorithm directly solves for the set of support labels that minimizes the KRR loss function, generating a unique dense label vector for each (natural) support image.
 |
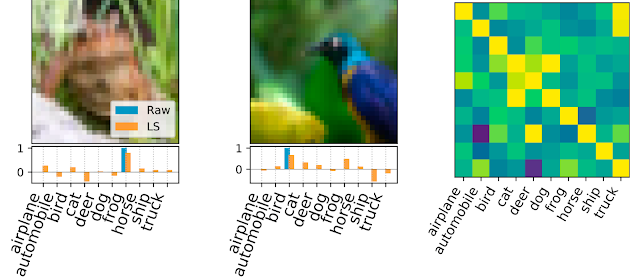| Example of labels obtained by label solving. Left and Middle: Sample images with possible labels listed below. The raw, one-hot label is shown in blue and the final LS generated dense label is shown in orange. Right: The covariance matrix between original labels and learned labels. Here, 500 labels were distilled from the CIFAR-10 dataset. A test accuracy of 69.7% is achieved using these labels for kernel ridge-regression. |
Distributed Computation
For simplicity, we focus on architectures that consist of convolutional neural networks with pooling layers. Specifically, we focus on the so-called “ConvNet” architecture and its variants because it has been featured in other dataset distillation studies. We used a slightly modified version of ConvNet that has a simple architecture given by three blocks of convolution, ReLu, and 2×2 average pooling and then a final linear readout layer, with an additional 3×3 convolution and ReLu layer prepended (see our GitHub for precise details).
 |
| ConvNet architecture used in DC/DSA. Ours has an additional 3×3 Conv and ReLu prepended. |
To compute the neural kernels needed in our work, we used the Neural Tangents library.
The first stage of this work, in which we applied KRR, focused on fully-connected networks, whose kernel elements are cheap to compute. But a hurdle facing neural kernels for models with convolutional layers plus pooling is that the computation of each kernel element between two images scales as the square of the number of input pixels (due to the capturing of pixel-pixel correlations by the kernel). So, for the second stage of this work, we needed to distribute the computation of the kernel elements and their gradients across many devices.
 |
| Distributed computation for large scale metalearning. |
We invoke a client-server model of distributed computation in which a server distributes independent workloads to a large pool of client workers. A key part of this is to divide the backpropagation step in a way that is computationally efficient (explained in detail in the paper).
We accomplish this using the open-source tools Courier (part of DeepMind’s Launchpad), which allows us to distribute computations across GPUs working in parallel, and JAX, for which novel usage of the jax.vjp function enables computationally efficient gradients. This distributed framework allows us to utilize hundreds of GPUs per distillation of the dataset, for both the KIP and LS algorithms. Given the compute required for such experiments, we are releasing our distilled datasets to benefit the wider research community.
Examples
Our first set of distilled images above used KIP to distill CIFAR-10 down to 1 image per class while keeping the labels fixed. Next, in the below figure, we compare the test accuracy of training on natural MNIST images, KIP distilled images with labels fixed, and KIP distilled images with labels optimized. We highlight that learning the labels provides an effective, albeit mysterious benefit to distilling datasets. Indeed the resulting set of images provides the best test performance (for infinite-width networks) despite being less interpretable.
 |
| MNIST dataset distillation with trainable and non-trainable labels. Top: Natural MNIST data. Middle: Kernel Inducing Point distilled data with fixed labels. Bottom: Kernel Inducing Point distilled data with learned labels. |
Results
Our distilled datasets achieve state-of-the-art performance on benchmark image classification datasets, improving performance beyond previous state-of-the-art models that used convolutional architectures, Dataset Condensation (DC) and Dataset Condensation with Differentiable Siamese Augmentation (DSA). In particular, for CIFAR-10 classification tasks, a model trained on a dataset consisting of only 10 distilled data entries (1 image / class, 0.02% of the whole dataset) achieves a 64% test set accuracy. Here, learning labels and an additional image preprocessing step leads to a significant increase in performance beyond the 50% test accuracy shown in our first figure (see our paper for details). With 500 images (50 images / class, 1% of the whole dataset), the model reaches 80% test set accuracy. While these numbers are with respect to neural kernels (using the KRR infinite width limit), these distilled datasets can be used to train finite-width neural networks as well. In particular, for 10 data points on CIFAR-10, a finite-width ConvNet neural network achieves 50% test accuracy with 10 images and 68% test accuracy using 500 images, which are still state-of-the-art results. We provide a simple Colab notebook demonstrating this transfer to a finite-width neural network.
 |
| Dataset distillation using Kernel Inducing Points (KIP) with a convolutional architecture outperforms prior state-of-the-art models (DC/DSA) on all benchmark settings on image classification tasks. Label Solve (LS, middle columns) while only distilling information in the labels could often (e.g. CIFAR-10 10, 50 data points per class) outperform prior state-of-the-art models as well. |
In some cases, our learned datasets are more effective than a natural dataset one hundred times larger in size.
Conclusion
We believe that our work on dataset distillation opens up many interesting future directions. For instance, our algorithms KIP and LS have demonstrated the effectiveness of using learned labels, an area that remains relatively underexplored. Furthermore, we expect that utilizing efficient kernel approximation methods can help to reduce computational burden and scale up to larger datasets. We hope this work encourages researchers to explore other applications of dataset distillation, including neural architecture search and continual learning, and even potential applications to privacy.
Anyone interested in the KIP and LS learned datasets for further analysis is encouraged to check out our papers [ICLR 2021, NeurIPS 2021] and open-sourced code and datasets available on Github.
Acknowledgement
This project was done in collaboration with Zhourong Chen, Roman Novak and Lechao Xiao. We would like to acknowledge special thanks to Samuel S. Schoenholz, who proposed and helped develop the overall strategy for our distributed KIP learning methodology.
